
二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点为A(﹣3,0)、B(1,0)两点,与y轴交于点C(0,﹣3m)(其中m>0),顶点为D.
(1)求该二次函数的解析式(系数用含m的代数式表示);
(2)如图①,当m=2时,点P为第三象限内的抛物线上的一个动点,设△APC的面积为S,试求出S与点P的横坐标x之间的函数关系式及S的最大值;
(3)如图②,当m取何值时,以A、D、C为顶点的三角形与△BOC相似?

(1)y= mx2+2mx﹣3m;(2)S与x之间的关系式为S=﹣3x2﹣9x,当x=﹣ 时,S有最大值为
时,S有最大值为 ;(3)当m=1时,以A、D、C为顶点的三角形与△BOC相似.
;(3)当m=1时,以A、D、C为顶点的三角形与△BOC相似.
【解析】
试题分析:(1)利用交点式求出抛物线的解析式.
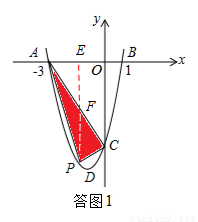
(2)如答图1,求出S的表达式,再根据二次函数的性质求出最值.
(3)△ACD与△BOC相似,且△BOC为直角三角形,所以△ACD必为直角三角形.本问分多种情形,需要分类讨论,避免漏解.
试题解析:【解析】
(1)∵抛物线与x轴交点为A(﹣3,0)、B(1,0),
∴可设抛物线解析式为:y=a(x+3)(x﹣1).
将点C(0,﹣3m)代入上式,得a×3×(﹣1)=﹣3m,∴a = m备.
∴抛物线的解析式为:y=m(x+3)(x﹣1)=mx2+2mx﹣3m.
(2)当m=2时,C(0,﹣6),抛物线解析式为y=2x2+4x﹣6,则P(x,2x2+4x﹣6).
设直线AC的解析式为y=kx+b,则有
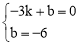 ,解得
,解得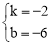 .
.
∴直线AC的解析式为y=﹣2x﹣6.
如答图1,过点P作PE⊥x轴于点E,交AC于点F,
则F(x,﹣2x﹣6).
∴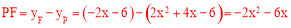 .
.
∴S=S△PFA+S△PFC= PF•AE+
PF•AE+ PF•OE=
PF•OE= PF•OA
PF•OA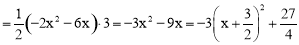 .
.
∴S与x之间的关系式为S=﹣3x2﹣9x,当x=﹣ 时,S有最大值为
时,S有最大值为 .
.
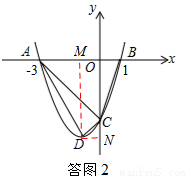
(3)∵y=mx2+2mx﹣3m=m(x+1)2﹣4m,∴顶点D坐标为(﹣1,﹣4m).
如答图2,过点D作DM⊥x轴于点M,则DM=4m,OM=1,AM=OA﹣OM=2;
过点D作DN⊥y轴于点N,则DN=1,CN=ON﹣OC=4m﹣3m=m.
由勾股定理得:AC2=OC2+OA2=9m2+9;CD2=CN2+DN2=m2+1;AD2=DM2+AM2=16m2+4.
∵△ACD与△BOC相似,且△BOC为直角三角形,
∴△ACD必为直角三角形.
i)若点A为直角顶点,则AC2+AD2=CD2,
即:(9m2+9)+(16m2+4)=m2+1,
整理得:m2=﹣ .∴此种情形不存在.
.∴此种情形不存在.
ii)若点D为直角顶点,则AD2+CD2=AC2,
即:(16m2+4)+(m2+1)=9m2+9,整理得:m2= ,
,
∵m>0,∴m=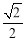 .
.
此时,可求得△ACD的三边长为: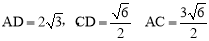 ,
,
△BOC的三边长为: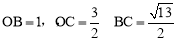 ,
,
∴两个三角形对应边不成比例,不可能相似.∴此种情形不存在.
iii)若点C为直角顶点,则AC2+CD2=AD2,
即:(9m2+9)+(m2+1)=16m2+4,整理得:m2=1,
∵m>0,∴m=1.
此时,可求得△ACD的三边长为: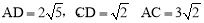 ,
,
△BOC的三边长为:OB=1,OC=3,BC=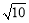 .
.
∵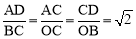 ,∴满足两个三角形相似的条件.
,∴满足两个三角形相似的条件.
∴m=1.
综上所述,当m=1时,以A、D、C为顶点的三角形与△BOC相似.
考点:1.二次函数综合题;2.单动点问题;3待定系数法的应用;4.曲线上点的坐标与方程的关系;5.二次函数的性质;6.由实际问题列函数关系式;7.勾股定理;8.相似三角形的判定;9.分类思想、转换思想和数形结合思想的应用.


科目:初中数学 来源:2014年初中毕业升学考试(湖南长沙卷)数学(解析版) 题型:填空题
如图,在平面直角坐标系中,已知点A(2,3),点B(﹣2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南邵阳卷)数学(解析版) 题型:选择题
如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )

A.45° B.54° C.40° D.50°
查看答案和解析>>
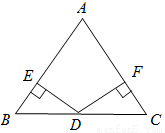
科目:初中数学 来源:2014年初中毕业升学考试(湖南衡阳卷)数学(解析版) 题型:解答题
如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F.
求证:△BED≌△CFD.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南衡阳卷)数学(解析版) 题型:填空题
甲、乙两同学参加学校运动员铅球项目选拔赛,各投掷6次,记录成绩,计算平均数和方差的结果为: ,则成绩较稳定的是 (填“甲”或“乙”).
,则成绩较稳定的是 (填“甲”或“乙”).
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南湘潭卷)数学(解析版) 题型:解答题
△ABC为等边三角形,边长为a,DF⊥AB,EF⊥AC,
(1)求证:△BDF∽△CEF;
(2)若a=4,设BF=m,四边形ADFE面积为S,求出S与m之间的函数关系,并探究当m为何值时S取最大值;
(3)已知A、D、F、E四点共圆,已知tan∠EDF= ,求此圆直径.
,求此圆直径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com