练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
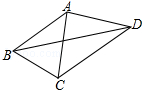
    15．如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=42°，则∠CAD的度数为（　　）
    A．110°B．88°C．84°D．66°

    分析 首先以A为圆心，AB长为半径画弧，然后可确定B、C、D同在⊙A上，再根据∠CBD=2∠BDC可得$\widehat{CD}$=2$\widehat{BC}$，然后可得∠CAD=2∠BAC=84°．

    解答 解：以A为圆心，AB长为半径画弧，
    ∵AB=AC=AD，
    ∴B、C、D同在⊙A上，
    ∵∠CBD=2∠BDC，
    ∴$\widehat{CD}$=2$\widehat{BC}$，
    ∴∠CAD=2∠BAC=84°，
    故选：C．

    点评 此题主要考查了圆周角定理，关键是掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．（1）用适当的语句表述图中的点A、B与直线l的关系；
    （2）读语句，画图形：点P是直线a外一点，过点P有一条直线b与直线a相交于点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列各组中，是同类项的是（　　）
    A．3x2y与3xy2B．3xy与-2xy2C．-2xy2与-2ab2D．0与π

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

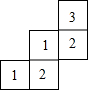    3．由一些棱长为1的小正方体搭成的几何体的俯视图如图所示，其正方形中的数字表示该位置上的小正方体的个数，画出该几何体的主视图和左视图（先用铅笔作出草图，确认无误后，再用签字笔勾线）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．解方程：
    （1）$\frac{2x-1}{3}-\frac{2x-3}{4}=1$
    （2）$\frac{x+4}{5}-x+5=\frac{x+3}{3}-\frac{x-2}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．一个三角形三个内角的度数之比为1：2：3，则这个三角形一定是（　　）
    A．等腰三角形B．锐角三角形C．直角三角形D．钝角三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．按括号内的要求取近似数：4.47876≈4.48（精确到百分位）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

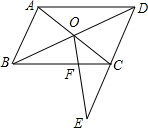    4．如图，在?ABCD中，对角线AC与BD相交于点O，在DC的延长线上取一点E，连接OE交BC于点F．已知AB=4，BC=6，CE=2，则CF的长等于（　　）
    A．1B．1.5C．2D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

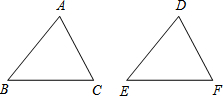    5．如图，在△ABC与△DEF中，已知AB=DE，∠A=∠D，还添加一个条件才能使△ABC≌△DEF，下列不能添加的条件是（　　）
    A．∠B=∠EB．BC=EFC．∠C=∠FD．AC=DF

    查看答案和解析>>

    同步练习册答案