
| 消费金额a(元)的范围 | 100≤a<400 | 400≤a<600 | 600≤a<800 |
| 获得奖券金额(元) | 40 | 100 | 130 |
分析 (1)先求出标价为800元的商品按80%的价格出售,消费金额为640元,再根据消费金额640元在600≤a<800之间,即可得出优惠额;
(2)分两种情况:当400≤a<600时;当600≤a<800时;讨论可求该顾客获得的优惠额;
(3)设购买标价为x元时,可以得到150的优惠额,根据(1)的计算方法列出方程解答即可.
解答 解:(1)800×80%=640元,
优惠额为800×(l-80%)+130=290元;
故答案为:640,290.
(2)消费金额在400≤a<600之间时,优惠额为(a÷80%)(1-80%)+100=$\frac{1}{4}$a+100;
消费金额在600≤a<800之间时,优惠额为(a÷80%)(1-80%)+130=$\frac{1}{4}$a+130;
(3)设该商品的消费金额为x元时,由题意得
在400≤a<600之间时,$\frac{1}{4}$x+100=150,解得x=200(舍去);
或在600≤a<800之间时,$\frac{1}{4}$x+130=150,解得x=80(不合题意,舍去).
答:她不能获得150元的优惠额.
点评 此题考查一元一次方程的实际运用,列代数式,理解题意,找出运算的方法是解决问题的关键.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 8 | B. | 4 | C. | 2 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
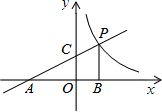 如图,直线$y=\frac{1}{2}x+2$分别交x轴、y轴于A、C两点,且与双曲线$y=\frac{k}{x}$在第一象限交于点P,作PB⊥x轴于B,S△ABP=9.
如图,直线$y=\frac{1}{2}x+2$分别交x轴、y轴于A、C两点,且与双曲线$y=\frac{k}{x}$在第一象限交于点P,作PB⊥x轴于B,S△ABP=9.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com