
把抛物线 先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为( )
先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为( )
A.  B.
B. 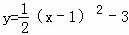 C.
C.  D.
D. 
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:初中数学 来源: 题型:
如图,△ABC是一块锐角三角形的材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少mm.
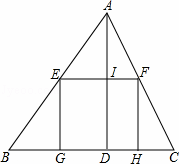
查看答案和解析>>
科目:初中数学 来源: 题型:
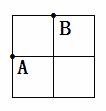
如图,在2×2的正方形网格中有9个格点,已经取定点A和点B,在余下的7个点中任取一点C,使△ABC为等腰直角三角形的概率是( )
A.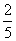 B.
B.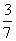 C.
C.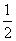 D.
D.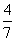
查看答案和解析>>
科目:初中数学 来源: 题型:
已知矩形ABCD中,AB=10cm,AD=4cm,作如下折叠操作.如图1和图2所示,在边AB上取点M,在边AD或边DC上取点P.连接MP.将△AMP或四边形AMPD沿着直线MP折叠得到△A′MP或四边形A′MPD′,点A的落点为点A′,点D的落点为点D′.
探究:
(1)如图1,若AM=8cm,点P在AD上,点A′落在DC上,则∠MA′C的度数为 ;
(2)如图2,若AM=5cm,点P在DC上,点A′落在DC上,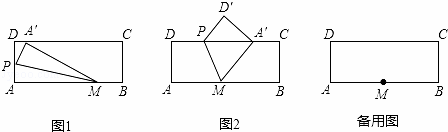
①求证:△MA′P是等腰三角形;
②直接写出线段DP的长.
(3)若点M固定为AB中点,点P由A开始,沿A﹣D﹣C方向.在AD,DC边上运动.设点P的运动速度为1cm/s,运动时间为ts,按操作要求折叠.
①求:当MA′与线段DC有交点时,t的取值范围;
②直接写出当点A′到边AB的距离最大时,t的值;
发现:
若点M在线段AB上移动,点P仍为线段AD或DC上的任意点.随着点M位置的不同.按操作要求折叠后.点A的落点A′的位置会出现以下三种不同的情况:
不会落在线段DC上,只有一次落在线段DC上,会有两次落在线段DC上.
请直接写出点A′由两次落在线段DC上时,AM的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com