
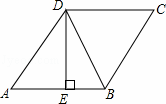
如图,在菱形ABCD中,DE⊥AB于点E,cosA=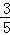 ,BE=4,则tan∠DBE的值是 .
,BE=4,则tan∠DBE的值是 .
2
考点: 菱形的性质;解直角三角形.
分析: 求出AD=AB,设AD=AB=5x,AE=3x,则5x﹣3x=4,求出x,得出AD=10,AE=6,在Rt△ADE中,由勾股定理求出DE=8,在Rt△BDE中得出tan∠DBE=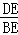 ,代入求出即可,
,代入求出即可,
解答: 解:∵四边形ABCD是菱形,
∴AD=AB,
∵cosA=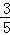 ,BE=4,DE⊥AB,
,BE=4,DE⊥AB,
∴设AD=AB=5x,AE=3x,
则5x﹣3x=4,
x=2,
即AD=10,AE=6,
在Rt△ADE中,由勾股定理得:DE=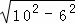 =8,
=8,
在Rt△BDE中,tan∠DBE= =
=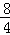 =2,
=2,
故答案为:2.
点评: 本题考查了菱形的性质,勾股定理,解直角三角形的应用,关键是求出DE的长.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
若反比例函数y=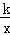 (k≠0)的图象经过点P(﹣2,3),则该函数的图象
(k≠0)的图象经过点P(﹣2,3),则该函数的图象
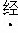
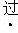 的点是( )
的点是( )
A. (3,﹣2) B. (1,﹣6) C. (﹣1,6) D. (﹣1,﹣6)
查看答案和解析>>
科目:初中数学 来源: 题型:
.设a、b是常数,且b>0,抛物线y=ax2+bx+a2﹣5a﹣6为下图中四个图象之一,则a的值为( )
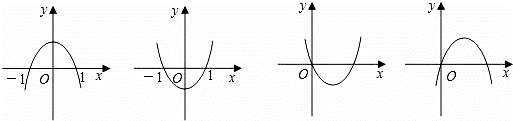
A. 6或﹣1 B. ﹣6或1 C. 6 D. ﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,美丽的徒骇河宛如一条玉带穿城而过,沿河两岸的滨河大道和风景带成为我市的一道新景观.在数学课外实践活动中,小亮在河西岸滨河大道一段AC上的A,B两点处,利用测角仪分别对东岸的观景台D进行了测量,分别测得∠DAC=60°,∠DBC=75°.又已知AB=100米,求观景台D到徒骇河西岸AC的距离约为多少米(精确到1米).(tan60°≈1.73,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,求证 (1)EF=CF;(2)∠DFE=3∠AEF.(8分)

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,王老师在上多边形外角和这节课时,做了一个活动,让小明在操场上从A点出发前进1m,向右转30°,再前进1m,又向右转30°,…,这样一直走下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.小明一共走了 m,这个多边形的内角和是 度.
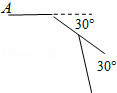
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com