
.设a、b是常数,且b>0,抛物线y=ax2+bx+a2﹣5a﹣6为下图中四个图象之一,则a的值为( )
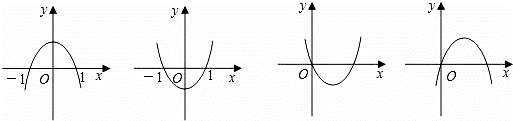
A. 6或﹣1 B. ﹣6或1 C. 6 D. ﹣1
D
考点: 二次函数的图象.
专题: 压轴题.
分析: 由b>0,排除前两个图象,第三个图象a>0,﹣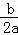 >0,推出b<0,与已知矛盾排除,从而抛物线y=ax2+bx+a2﹣5a﹣6的图象是第四个图,再求a的值.
>0,推出b<0,与已知矛盾排除,从而抛物线y=ax2+bx+a2﹣5a﹣6的图象是第四个图,再求a的值.
解答: 解:∵图1和图2表示y=0时,有1和﹣1两个根,代入方程能得出b=﹣b,即b=0,不合题意,
∴排除前两个图象;
∵第三个图象a>0,又﹣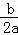 >0,
>0,
∴b<0,与已知矛盾排除,
∴抛物线y=ax2+bx+a2﹣5a﹣6的图象是第四个图,
由图象可知,抛物线经过原点(0,0),
∴a2﹣5a﹣6=0,解得a=﹣1或6,
∵a<0,∴a=﹣1.
故选D.
点评: 主要考查了从图象上把握有用的条件,准确选择数量关系解得a的值,简单的图象最少能反映出2个条件:开口方向,经过原点,利用这两个条件即可求出a的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
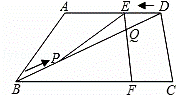
如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=4cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题:
(1)当t为何值时,PE∥AB;
(2)设△PEQ的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S△PEQ=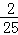 S△BCD?若存在,求出此时t的值;若不存在,说明理由;
S△BCD?若存在,求出此时t的值;若不存在,说明理由;
(4)连接PF,在上述运动过程中,五边形PFCDE的面积是否发生变化?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
把锐角△ABC的各边都扩大2倍得△A′B′C′,那么∠A、∠A′的余弦值关系是( )
A. cosA=cosA′ B. cosA=2cosA′ C. 2cosA=cosA′ D. 不确定的
查看答案和解析>>
科目:初中数学 来源: 题型:
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知点A是双曲线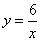 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第二象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第二象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线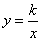 上运动,则
上运动,则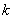 的值是 .
的值是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com