
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?

考点: 二次函数的应用.
专题: 销售问题.
分析: (1)设函数关系式y=kx+b,把(10,40),(18,24)代入求出k和b即可,由成本价为10元/千克,销售价不高于18元/千克,得出自变量x的取值范围;
(2)根据销售利润=销售量×每一件的销售利润得到w和x的关系,利用二次函数的性质得最值即可;
(3)先把y=150代入(2)的函数关系式中,解一元二次方程求出x,再根据x的取值范围即可确定x的值.
解答: 解:(1)设y与x之间的函数关系式y=kx+b,把(10,40),(18,24)代入得
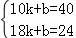 ,
,
解得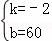 ,
,
∴y与x之间的函数关系式y=﹣2x+60(10≤x≤18);
(2)W=(x﹣10)(﹣2x+60)
=﹣2x2+80x﹣600,
对称轴x=20,在对称轴的左侧y随着x的增大而增大,
∵10≤x≤18,
∴当x=18时,W最大,最大为192.
即当销售价为18元时,每天的销售利润最大,最大利润是192元.
(3)由150=﹣2x2+80x﹣600,
解得x1=15,x2=25(不合题意,舍去)
答:该经销商想要每天获得150元的销售利润,销售价应定为15元.
点评: 本题考查了二次函数的应用,得到每天的销售利润的关系式是解决本题的关键,结合实际情况利用二次函数的性质解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
.设a、b是常数,且b>0,抛物线y=ax2+bx+a2﹣5a﹣6为下图中四个图象之一,则a的值为( )
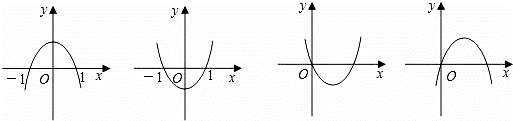
A. 6或﹣1 B. ﹣6或1 C. 6 D. ﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
已知函数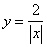 的图象在第一象限的一支曲线上有一点A(a,c+1),在该函数图象的另外一支上有点B(b,c),则关于一元二次方程ax2+bx+c=0的两根x1,x2判断正确的是( )
的图象在第一象限的一支曲线上有一点A(a,c+1),在该函数图象的另外一支上有点B(b,c),则关于一元二次方程ax2+bx+c=0的两根x1,x2判断正确的是( )
A.0<x1+x2<1,x1•x2>0 B.x1+x2<0,x1•x2>0
C.x1+x2>1,x1•x2>0 D.x1+x2与x1•x2的符号都不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过转转盘获得购物券.规定顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准100元、50元、20元的相应区域,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果指针对准其它区域,那么就不能获得购物券.另一种方式是:不转转盘,顾客每购买100元的商品,可直接获得10元购物券.据统计,一天中共有1000人次选择了转转盘的方式,其中指针落在100元、50元、20元的次数分别为50次、100次、200次.
(1)指针落在不获奖区域的概率约是多少?
(2)通过计算说明选择哪种方式更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com