练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    △ABC的内切圆半径为2cm，△ABC的周长为5cm，则△ABC的面积是　cm2．


    　5

    考点： 三角形的内切圆与内心． 

    分析： 连OA，OB，OC．把三角形ABC分成三个三角形，根据内心的性质和三角形面积公式用三个三角形的面积的和表示三角形ABC面积，计算即可．

    解答： 解：如图，⊙O是△ABC的内切圆，切点分别为D，E，F．

    连OA，OB，OC，OD，OE，OF．

    则OD⊥AB，OE⊥BC，OF⊥AC，且OE=OF=OD=2，

    S△ABC=S△AOB+S△OBC+S△OAC

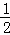    =×2×AB+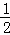×2×B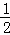C+×2×AC

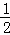    =（AB+AC+BC）×2=5，

    故答案为：5．

    点评： 本题考查的是三角形的内心的性质，掌握三角形的内心是三角形三条角平分线的交点是解题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


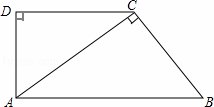
    如图，在直角梯形ABCD中，AB∥DC，∠D=90°，AC⊥BC，AB=10cm，BC=6cm，

    （1）求证：△ACD∽△BAC；

    （2）求DC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知m和n是方程2x2﹣5x﹣3=0的两根，则+的值是（　　）

    　 A． ﹣2 B． 2 C． ﹣ D． 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


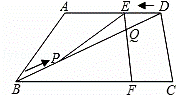
    如图，在梯形ABCD中，AD∥BC，AD=6cm，CD=4cm，BC=BD=10cm，点P由B出发沿BD方向匀速运动，速度为1cm/s；同时，线段EF由DC出发沿DA方向匀速运动，速度为1cm/s，交BD于Q，连接PE．若设运动时间为t（s）（0＜t＜5）．解答下列问题：

    （1）当t为何值时，PE∥AB；

    （2）设△PEQ的面积为y（cm2），求y与t之间的函数关系式；

    （3）是否存在某一时刻t，使S△PEQ=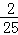S△BCD？若存在，求出此时t的值；若不存在，说明理由；

    （4）连接PF，在上述运动过程中，五边形PFCDE的面积是否发生变化？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    用如图所示的扇形纸片制作一个圆锥的侧面，要求圆锥的高是4cm，底面周长是6πcm，则扇形的半径为（　　）

    　 A． 3cm B． 5cm C． 6cm D． 8cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ．已知直线y=kx（k＞0）与双曲线交于A（x1，y1），B（x2，y2）两点，则2x1y2﹣7x2y1=　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


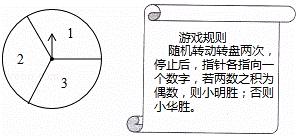
    如图所示，可以自由转动的转盘被3等分，指针落在每个扇形内的机会均等．

    （1）现随机转动转盘一次，停止后，指针指向1的概率为　　；

    （2）小明和小华利用这个转盘做游戏，若采用下列游戏规则，你认为对双方公平吗？请用列表或画树状图的方法说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    比较大小：2　　﹣3．（用“＞”或“＜”或“=”填空）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某经销商销售一种产品，这种产品的成本价为10元/千克，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于18元/千克，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）之间的函数关系如图所示：

    （1）求y与x之间的函数关系式，并写出自变量x的取值范围；

    （2）求每天的销售利润W（元）与销售价x（元/千克）之间的函数关系式．当销售价为多少时，每天的销售利润最大？最大利润是多少？

    （3）该经销商想要每天获得150元的销售利润，销售价应定为多少？

    查看答案和解析>>

    同步练习册答案