
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,
(1)求证:△ACD∽△BAC;
(2)求DC的长.
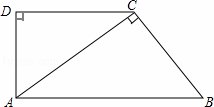
考点: 相似三角形的判定与性质;直角梯形.
分析: (1)由CD∥AB,得∠DCA=∠CAB,加上一组直角,即可证得所求的三角形相似.
(2)在Rt△ABC中,由勾股定理可求得AC的长,根据(1)题所得相似三角形的比例线段,即可求出DC的长.
解答: 解:(1)∵CD∥AB,
∴∠BAC=∠DCA,
又∵AC⊥BC,
∴∠ACB=90°,
∴∠D=∠ACB=90°,
∴△ACD∽△BAC;
(2)Rt△ABC中,AC=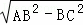 =8cm,
=8cm,
∵△ACD∽△BAC,
∴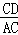 =
=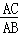 ,
,
即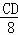 =
= ,
,
解得:DC=6.4cm.
点评: 此题考查了梯形的性质、相似三角形的判定和性质、勾股定理、熟练掌握相似三角形的判定和性质定理是解题的关键.


科目:初中数学 来源: 题型:
中国海军参加打击索马里海盗的护航行动,舰载直升飞机发现海盗船后,从舰艇上方海拔300米的位置平飞,突然发现前方有气流,就以30米/秒的速度上升50秒,平飞3分钟后,又以12米/秒速度下降80秒接近海盗船,问这时直升飞机的高度是海拔多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
.下列方程中一定是一元二次方程的是( )
A. ax2﹣bx=0 B. 2x2+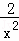 ﹣2=0
﹣2=0
C. (x﹣2)(3x+1)=0 D. 3x2﹣2x=3(x+1)(x﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
我们知道任何实数的平方一定是一个非负数,即:(a+b)2≥0,且﹣(a+b)2≤0.据此,我们可以得到下面的推理:
∵x2+2x+3=(x2+2x+1)+2=(x+1)2+2,而(x+1)2≥0
∴(x+1)2+2≥2,故x2+2x+3的最小值是2.
试根据以上方法判断代数式3y2﹣6y+11是否存在最大值或最小值?若有,请求出它的最大值或最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com