
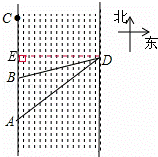
如图,美丽的徒骇河宛如一条玉带穿城而过,沿河两岸的滨河大道和风景带成为我市的一道新景观.在数学课外实践活动中,小亮在河西岸滨河大道一段AC上的A,B两点处,利用测角仪分别对东岸的观景台D进行了测量,分别测得∠DAC=60°,∠DBC=75°.又已知AB=100米,求观景台D到徒骇河西岸AC的距离约为多少米(精确到1米).(tan60°≈1.73,tan75°≈3.73)
考点: 解直角三角形的应用.
专题: 几何图形问题;数形结合.
分析: 如图,过点D作DE⊥AC于点E.通过解Rt△EAD和Rt△EBD分别求得AE、BE的长度,然后根据图示知:AB=AE﹣BE=100,把相关线段的长度代入列出关于ED的方程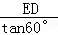 ﹣
﹣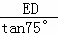 =100.通过解该方程求得ED的长度.
=100.通过解该方程求得ED的长度.
解答: 解:如图,过点D作DE⊥AC于点E.
∵在Rt△EAD中,∠DAE=60°,
∴tan60°=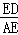 ,
,
∴AE=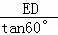
同理,在Rt△EBD中,
得到EB=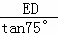 .
.
又∵AB=100米,
∴AE﹣EB=100米,
即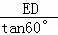 ﹣
﹣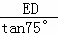 =100.
=100.
则ED=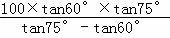 ≈
≈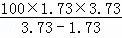 ≈323(米).
≈323(米).
答:观景台D到徒骇河西岸AC的距离约为323米.
点评: 本题考查了解直角三角形的应用.主要是正切概念及运算,关键把实际问题转化为数学问题加以计算.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
一圆锥体形状的水晶饰品,母线长是10cm,底面圆的直径是5cm,点A为圆锥底面圆周上一点,从A点开始绕圆锥侧面缠一圈彩带回到A点,则彩带最少用多少厘米(接口处重合部分忽略不计)( )
A. 10πcm B. 10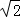 cm C. 5πcm D. 5
cm C. 5πcm D. 5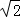 cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么
(1)设△POQ的面积为y,求y关于t的函数解析式;
(2)当△POQ的面积最大时,将△POQ沿直线PQ翻折后得到△PCQ,试判断点C是否落在直线AB上,并说明理由;
(3)当t为何值时,△POQ与△AOB相似.

查看答案和解析>>
科目:初中数学 来源: 题型:
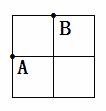
如图,在2×2的正方形网格中有9个格点,已经取定点A和点B,在余下的7个点中任取一点C,使△ABC为等腰直角三角形的概率是( )
A.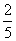 B.
B.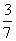 C.
C.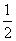 D.
D.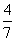
查看答案和解析>>
科目:初中数学 来源: 题型:
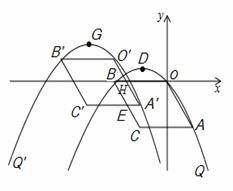
如图,在平面直角坐标系xOy中,四边形OACB是平行四边形,A、B两点的坐标分别为(2,﹣4),(﹣4,0),抛物线Q经过O、A、B三点,D是抛物线Q的顶点.
(1)求抛物线Q的解析式及顶点D的坐标;
(2)将抛物线Q和平行四边形OACB一起先向左平移4个单位后,再向上平移m(0<m<3)个 单位,得到抛物线Q′和平行四边形O′A′C′B′,在向下平移的过程中,设平行四边形O′A′C′B′与平
单位,得到抛物线Q′和平行四边形O′A′C′B′,在向下平移的过程中,设平行四边形O′A′C′B′与平 行四边形OACB的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;
行四边形OACB的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;
(3)在(2)的条件下,当S取最大值时,设此时抛物线Q′的顶点为G,若点M是x轴上的动点,点N是抛物线Q′上的动点,试判断是否存在这样的点M和点N,使得以D、G、M、N为顶点的四边形是平行四边形?若存在,请求出点所有的M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
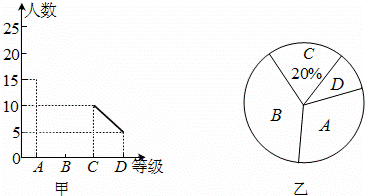
“中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)共抽取了多少个学生进行调查?
(2)将图甲中的折线统计图补充完整.
(3)求出图乙中B等级所占圆心角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com