
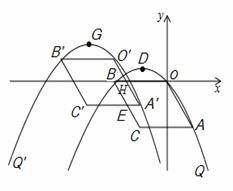
如图,在平面直角坐标系xOy中,四边形OACB是平行四边形,A、B两点的坐标分别为(2,﹣4),(﹣4,0),抛物线Q经过O、A、B三点,D是抛物线Q的顶点.
(1)求抛物线Q的解析式及顶点D的坐标;
(2)将抛物线Q和平行四边形OACB一起先向左平移4个单位后,再向上平移m(0<m<3)个 单位,得到抛物线Q′和平行四边形O′A′C′B′,在向下平移的过程中,设平行四边形O′A′C′B′与平
单位,得到抛物线Q′和平行四边形O′A′C′B′,在向下平移的过程中,设平行四边形O′A′C′B′与平 行四边形OACB的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;
行四边形OACB的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;
(3)在(2)的条件下,当S取最大值时,设此时抛物线Q′的顶点为G,若点M是x轴上的动点,点N是抛物线Q′上的动点,试判断是否存在这样的点M和点N,使得以D、G、M、N为顶点的四边形是平行四边形?若存在,请求出点所有的M的坐标;若不存在,请说明理由.
科目:初中数学 来源: 题型:
数轴上表示整数的点称为整点.某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2009厘米的线段AB,则线段AB盖住的整点的个数是( )
A. 2007或2008 B. 2008或2009 C. 2009或2010 D. 2010或2011
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,美丽的徒骇河宛如一条玉带穿城而过,沿河两岸的滨河大道和风景带成为我市的一道新景观.在数学课外实践活动中,小亮在河西岸滨河大道一段AC上的A,B两点处,利用测角仪分别对东岸的观景台D进行了测量,分别测得∠DAC=60°,∠DBC=75°.又已知AB=100米,求观景台D到徒骇河西岸AC的距离约为多少米(精确到1米).(tan60°≈1.73,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,求证 (1)EF=CF;(2)∠DFE=3∠AEF.(8分)

查看答案和解析>>
科目:初中数学 来源: 题型:
若关于x的一元二次方程kx2﹣4x+2=0有两个不相等的实数根,则k的取值范围是( )
A. k<2 B. k≠0 C. k<2且k≠0 D. k>2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知平行四边形ABCD中,AB=5,BC=8,cosB= ,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
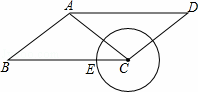
A. 0<CE≤8 B. 0<CE≤5
C. 0<CE<3或5<CE≤8 D. 3<CE≤5
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的盒子中装有12个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率是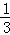 ,则黄球的个数为( )
,则黄球的个数为( )
A. 18 B. 20 C. 24 D. 28
查看答案和解析>>
科目:初中数学 来源: 题型:
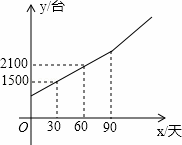
随着生活质量的提高,人们健康意识逐渐增强,安装净水设备的百姓家庭越来越多.某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示.今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
(1)求y与x之间的函数表达式;
(2)已知该厂家去年平均每天的生产数量与今年前90天平均每天的生产数量相同,求厂家去年生产的天数;
(3)如果厂家制定总量不少于6000台的生产计划,那么在改进技术后,至少还要多少天完成生产计划?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com