
随着生活质量的提高,人们健康意识逐渐增强,安装净水设备的百姓家庭越来越多.某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示.今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
(1)求y与x之间的函数表达式;
(2)已知该厂家去年平均每天的生产数量与今年前90天平均每天的生产数量相同,求厂家去年生产的天数;
(3)如果厂家制定总量不少于6000台的生产计划,那么在改进技术后,至少还要多少天完成生产计划?
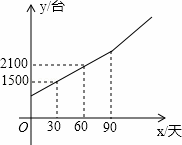
考点: 一次函数的应用;一元一次不等式的应用.
专题: 应用题;分段函数.
分析: (1)本题是一道分段函数,当0≤x≤90时和x>90时由待定系数法就可以分别求出其结论;
(2)由(1)的解析式求出今年前90天平均每天的生产数量,由函数图象可以求出去年的生产总量就可以得出结论;
(3)设改进技术后,至少还要a天完成不少于6000台的生产计划,根据前90天的生产量+改进技术后的生产量≥6000建立不等式求出其解即可.
解答: 解:(1)当0≤x≤90时,设y与x之间的函数关系式为y=kx+b,由函数图象,得
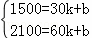 ,
,
解得: .
.
则y=20x+900.
当x>90时,由题意,得y=30x.
∴y=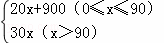 ;
;
(2)由题意,得
∵x=0时,y=900,
∴去年的生产总量为900台.
今年平均每天的生产量为:(2700﹣900)÷90=20台,
厂家去年生产的天数为:900÷20=45天.
答:厂家去年生产的天数为45天;
(3)设改进技术后,还要a天完成不少于6000台的生产计划,由题意,得
2700+30a≥6000,
解得:a≥110.
答:改进技术后,至少还要110天完成不少于6000台的生产计划.
点评: 本题考查了分段函数的运用,待定系数法起一次函数的解析式的运用,列不等式解实际问题的运用,解答时求出一次函数的解析式及分析函数图象的意义是关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
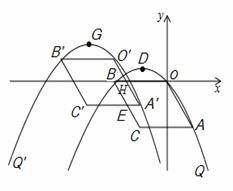
如图,在平面直角坐标系xOy中,四边形OACB是平行四边形,A、B两点的坐标分别为(2,﹣4),(﹣4,0),抛物线Q经过O、A、B三点,D是抛物线Q的顶点.
(1)求抛物线Q的解析式及顶点D的坐标;
(2)将抛物线Q和平行四边形OACB一起先向左平移4个单位后,再向上平移m(0<m<3)个 单位,得到抛物线Q′和平行四边形O′A′C′B′,在向下平移的过程中,设平行四边形O′A′C′B′与平
单位,得到抛物线Q′和平行四边形O′A′C′B′,在向下平移的过程中,设平行四边形O′A′C′B′与平 行四边形OACB的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;
行四边形OACB的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;
(3)在(2)的条件下,当S取最大值时,设此时抛物线Q′的顶点为G,若点M是x轴上的动点,点N是抛物线Q′上的动点,试判断是否存在这样的点M和点N,使得以D、G、M、N为顶点的四边形是平行四边形?若存在,请求出点所有的M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
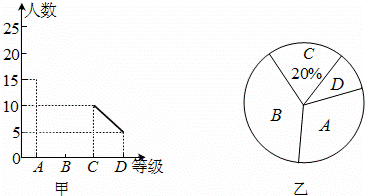
“中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)共抽取了多少个学生进行调查?
(2)将图甲中的折线统计图补充完整.
(3)求出图乙中B等级所占圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
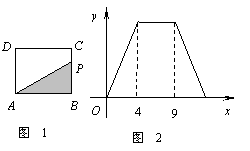
 如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是
如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是
A.18
 B.16
B.16
C.10
D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com