
一圆锥体形状的水晶饰品,母线长是10cm,底面圆的直径是5cm,点A为圆锥底面圆周上一点,从A点开始绕圆锥侧面缠一圈彩带回到A点,则彩带最少用多少厘米(接口处重合部分忽略不计)( )
A. 10πcm B. 10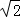 cm C. 5πcm D. 5
cm C. 5πcm D. 5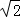 cm
cm
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
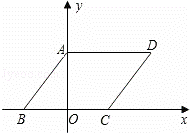
如图,▱ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB.
(1)求sin∠ABC的值;
(2)若E为x轴上的点,且S△AOE=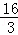 ,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
若反比例函数y=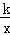 (k≠0)的图象经过点P(﹣2,3),则该函数的图象
(k≠0)的图象经过点P(﹣2,3),则该函数的图象
 的点是( )
的点是( )
A. (3,﹣2) B. (1,﹣6) C. (﹣1,6) D. (﹣1,﹣6)
查看答案和解析>>
科目:初中数学 来源: 题型:
从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数 100 400 800 1000 2000 5000
发芽种子粒数 85 298 652 793 1604 4005
发芽频率 0.850 0.745 0.815 0.793 0.802 0.801
根据以上数据可以估计,该玉米种子发芽的概率约为 (精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
数轴上表示整数的点称为整点.某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2009厘米的线段AB,则线段AB盖住的整点的个数是( )
A. 2007或2008 B. 2008或2009 C. 2009或2010 D. 2010或2011
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,美丽的徒骇河宛如一条玉带穿城而过,沿河两岸的滨河大道和风景带成为我市的一道新景观.在数学课外实践活动中,小亮在河西岸滨河大道一段AC上的A,B两点处,利用测角仪分别对东岸的观景台D进行了测量,分别测得∠DAC=60°,∠DBC=75°.又已知AB=100米,求观景台D到徒骇河西岸AC的距离约为多少米(精确到1米).(tan60°≈1.73,tan75°≈3.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com