
如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么
(1)设△POQ的面积为y,求y关于t的函数解析式;
(2)当△POQ的面积最大时,将△POQ沿直线PQ翻折后得到△PCQ,试判断点C是否落在直线AB上,并说明理由;
(3)当t为何值时,△POQ与△AOB相似.

考点: 二次函数综合题.
专题: 综合题;压轴题.
分析: (1)根据P、Q的速度,用时间t表示出OQ和OP的长,即可通过三角形的面积公式得出y,t的函数关系式;
(2)先根据(1)的函数式求出y最大时,x的值,即可得出OQ和OP的长,然后求出C点的坐标和直线AB的解析式,将C点坐标代入直线AB的解析式中即可判断出C是否在AB上;
(3)本题要分△OPQ∽△OAB和△OPQ∽△OBA两种情况进行求解,可根据各自得出的对应成比例相等求出t的值.
解答: 解:(1)∵OA=12,OB=6,由题意,得BQ=1×t=t,OP=1×t=t.
∴OQ=6﹣t.
∴y=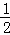 ×OP×OQ=
×OP×OQ=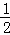 ×t(6﹣t)=﹣
×t(6﹣t)=﹣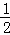 t2+3t(0≤t≤6);
t2+3t(0≤t≤6);
(2)∵y=﹣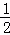 t2+3t,
t2+3t,
∴当y有最大值时,t=3
∴OQ=3,OP=3,即△POQ是等腰直角三角形.
把△POQ沿直线PQ翻折后,可得四边形OPCQ是正方形.
∴点C的坐标为(3,3).
∵A(12,0),B(0,6),
∴直线AB的解析式为y=﹣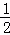 x+6
x+6
当x=3时,y=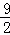 ≠3,
≠3,
∴点C不落在直线AB上;
(3)
①若△POQ∽△AOB时,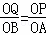 ,即
,即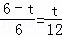 ,12﹣2t=t,∴t=4.
,12﹣2t=t,∴t=4.
②若△POQ∽△BOA时,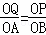 ,即
,即 ,6﹣t=2t,∴t=2.
,6﹣t=2t,∴t=2.
∵0≤t≤6,
∴t=4和t=2均符合题意,
∴当t=4或t=2时,△POQ与△AOB相似.
点评: 本题主要考查了直角三角形的性质、图形的翻折变换、相似三角形的判定和性质等知识点.要注意(3)题要根据不同的相似三角形分类进行讨论.


科目:初中数学 来源: 题型:
从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数 100 400 800 1000 2000 5000
发芽种子粒数 85 298 652 793 1604 4005
发芽频率 0.850 0.745 0.815 0.793 0.802 0.801
根据以上数据可以估计,该玉米种子发芽的概率约为 (精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
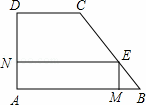
如图,直角梯形ABCD中,∠A=90°,∠B=45°,底边AB=5,高AD=3,点E由B沿折线BCD向点D移动,EM⊥AB于M,EN⊥AD于N,设BM=x,矩形AMEN的面积为y,那么y与x之间的函数关系的图象大致是( )
A. 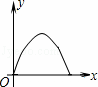 B.
B. 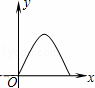 C.
C. 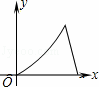 D.
D. 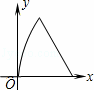
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,美丽的徒骇河宛如一条玉带穿城而过,沿河两岸的滨河大道和风景带成为我市的一道新景观.在数学课外实践活动中,小亮在河西岸滨河大道一段AC上的A,B两点处,利用测角仪分别对东岸的观景台D进行了测量,分别测得∠DAC=60°,∠DBC=75°.又已知AB=100米,求观景台D到徒骇河西岸AC的距离约为多少米(精确到1米).(tan60°≈1.73,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
若关于x的一元二次方程kx2﹣4x+2=0有两个不相等的实数根,则k的取值范围是( )
A. k<2 B. k≠0 C. k<2且k≠0 D. k>2
查看答案和解析>>
科目:初中数学 来源: 题型:
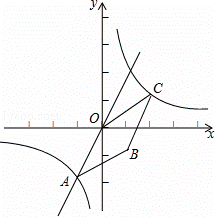
如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移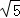 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com