
如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移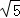 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
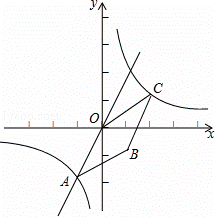
考点: 反比例函数综合题.
分析: (1)设反比例函数的解析式为y= (k>0),然后根据条件求出A点坐标,再求出k的值,进而求出反比例函数的解析式;
(k>0),然后根据条件求出A点坐标,再求出k的值,进而求出反比例函数的解析式;
(2)直接由图象得出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)首先求出OA的长度,结合题意CB∥OA且CB=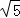 ,判断出四边形OABC是平行四边形,再证明OA=OC即可判定出四边形OABC的形状.
,判断出四边形OABC是平行四边形,再证明OA=OC即可判定出四边形OABC的形状.
解答: 解:(1)设反比例函数的解析式为y=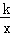 (k>0),
(k>0),
∵A(m,﹣2)在y=2x上,
∴﹣2=2m,
∴m=﹣1,
∴A(﹣1,﹣2),
又∵点A在y=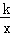 上,
上,
∴k=2,
∴反比例函数的解析式为y= ;
;
(2)观察图象可知正比例函数值大于反比例函数值时自变量x的取值范围为﹣1<x<0或x>1;
(3)四边形OABC是菱形.
证明:∵A(﹣1,﹣2),
∴OA=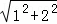 =
=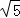 ,
,
由题意知:CB∥OA且CB=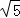 ,
,
∴CB=OA,
∴四边形OABC是平行四边形,
∵C(2,n)在y= 上,
上,
∴n=1,
∴C(2,1),
OC=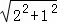 =
= ,
,
∴OC=OA,
∴四边形OABC是菱形.
点评: 本题主要考查了反比例函数的综合题的知识点,解答本题的关键是熟练掌握反比例函数的性质以及菱形的判定定理,此题难度不大,是一道不错的中考试题.


科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么
(1)设△POQ的面积为y,求y关于t的函数解析式;
(2)当△POQ的面积最大时,将△POQ沿直线PQ翻折后得到△PCQ,试判断点C是否落在直线AB上,并说明理由;
(3)当t为何值时,△POQ与△AOB相似.

查看答案和解析>>
科目:初中数学 来源: 题型:
“中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)共抽取了多少个学生进行调查?
(2)将图甲中的折线统计图补充完整.
(3)求出图乙中B等级所占圆心角的度数.
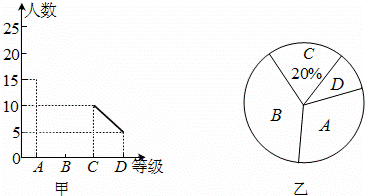
查看答案和解析>>
科目:初中数学 来源: 题型:
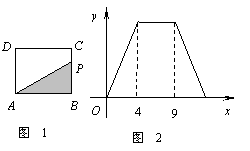
 如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是
如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是
A.18
 B.16
B.16
C.10
D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com