
分析 当x3+y3+z3+mxyz能被x+y+z整除时,它含有x+y+z 因式,运用赋值法即可求解.
解答 解:当x3+y3+z3+mxyz能被x+y+z整除时,它含有x+y+z 因式,
令x+y+z=0,得x=-(y+z),代入原式其值必为0,
即[-(y+z)]3+y3+z3-myz(y+z)=0,
把左边因式分解,得-yz(y+z)(m+3)=0,
∵xyz≠0,
∴x≠0,
∵x=-(y+z),
∴(y+z)≠0,
∴当m+3=0时等式成立,
∴当m=-3时,x,y,z不论取什么值,原式都能被x+y+z整除.
点评 此题考查了整式的除法,本题用到的其实还是逆推,要想整除必定含有x+y+z这个因式,然后巧妙的运用赋值法降低解题难度.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两对角线相等的四边形是矩形 | |
| B. | 两对角线互相平分的四边形是平行四边形 | |
| C. | 两对角线互相垂直的四边形是菱形 | |
| D. | 两对角线互相垂直且平分的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
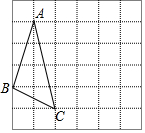 如图网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,建立适当的坐标系,使得B、C两点的坐标分别为B(-1,-1),C(1,-2),将△ABC绕点C顺时针旋转90°,得到△A′B′C′.
如图网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,建立适当的坐标系,使得B、C两点的坐标分别为B(-1,-1),C(1,-2),将△ABC绕点C顺时针旋转90°,得到△A′B′C′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com