
����Ŀ���Ķ����в��ϣ�Ȼ�������⣮
�������ı���(��������)�������Բ����������ı��ε����Բ��Բ�������ı��εĶԳ����ģ�������ı��ν������Բ���ڽ����ı�����
��ͼ��������ABCD�ڽ��ڡ�O����O�����ΪS1��������ABCD�����ΪS2����Բ��OΪ��������MON��ʹ��MON��90��������MON�Ƶ�O��ת��OM��ON�ֱ����O���ڵ�E��F���ֱ���������ABCD�ı߽��ڵ�G��H������OE��OF��![]() ��������ABCD�ı�Χ�ɵ�ͼ��(��Ӱ����)�����ΪS��
��������ABCD�ı�Χ�ɵ�ͼ��(��Ӱ����)�����ΪS��
��1����OM������Aʱ(��ͼ��)����S��S1��S2֮��Ĺ�ϵΪ�� (�ú�S1��S2�Ĵ���ʽ��ʾ)��
��2����OM��AB��Gʱ(��ͼ��)����(1)�еĽ�����Ȼ��������˵�����ɣ�
��3������MON��ת������λ��ʱ����ͼ�ۣ�����1���еĽ�����Ȼ��������˵������.

���𰸡���1��![]() ��
��
��2����1���еĽ�����Ȼ���������ɼ�������
��2����1���еĽ�����Ȼ���������ɼ�����.
�������������������1����������ε����ʼ�����ֱ�������ε����ʣ����ó����ۣ�
��2����Ȼ��������֤���ı���OGHBΪ�����Σ���������Ӱ���ֵ����Ϊ����OEF�������ȥ������OGBH�������
��3����Ȼ��������O��OR��AB��OS��BC������ֱ�ΪR��S�����֤����ORG�ա�OSH���ɵó��ı���ORBS�����=�ı���OGBH�����������������OEF�������������ORBS��������ɵó����ۣ�
�����������1����OM������Aʱ�������ε����ʿ�֪����MON=90����
��S��OAB=![]() S������ABCD=
S������ABCD=![]() S2��S����OEF=
S2��S����OEF=![]() SԲO=
SԲO=![]() S1��
S1��
��S=S����OEF-S��OAB=![]() SԲO-
SԲO-![]() S������ABCD=
S������ABCD=![]() S1-
S1-![]() S2=
S2=![]() ��S1-S2����
��S1-S2����
��2��������Ȼ�������������£�
�ߡ�EOF=90����
��S����OEF=![]() SԲO=
SԲO=![]() S1
S1
�ߡ�OGB=��EOF=��ABC=90����
���ı���OGBHΪ���Σ�
��OM��AB��
��BG=![]() AB=
AB=![]() BC=BH��
BC=BH��
���ı���OGBHΪ�����Σ�
��S�ı���OGBH=BG2=��![]() AB��2=
AB��2=![]() S2��
S2��
��S=S����OEF-S�ı���OGBH=![]() S1-
S1-![]() S2=
S2=![]() ��S1-S2����
��S1-S2����
��3����1���еĽ�����Ȼ�������������£�
�ߡ�EOF=90����
��S����OEF=![]() SԲO=
SԲO=![]() ��
��
��O��OR��AB��OS��BC������ֱ�ΪR��S��
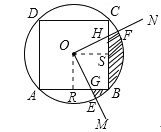
�ɣ�2����֪�ı���ORBSΪ�����Σ�
��OR=OS��
�ߡ�ROS=90������MON=90����
���ROG=��SOH=90��-��GOS��
����ROG����SOH��
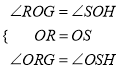 ��
��
���ROG�ա�SOH��ASA����
��S��ORG=S��OSH��
��S�ı���OGBH=S������ORBS��
�ɣ�2����֪S������ORBS=![]() S2��
S2��
��S�ı���OGBH=![]() S2��
S2��
��S=S����OEF-S�ı���OGBH=![]() ��S1-S2����
��S1-S2����


 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=x+2��������y=ax2+bx+6��a��0���ཻ��A��![]() ��
��![]() ����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��
����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��

��1���������ߵĽ���ʽ��
��2���Ƿ����������P�㣬ʹ�߶�PC�ij������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
��3����PACΪֱ��������ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������˶���ʽ������ת����( )
A. �ڿ��������������� B. �ɳ۵Ļ�
C. ʱ�����Ӱڵİڶ� D. �˶�Ա�����ı�ǹ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ж�һԪ���η���x2+x��3=0����������жϣ���ȷ���ǣ�������
A. �����������ʵ���� B. ���������ʵ����
C. ����ֻ��һ��ʵ���� D. û��ʵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ε����߳��ֱ�Ϊ3��6�������ߵı߳��Ƿ��̣�x��2����x��4��=0�ĸ�������������ε��ܳ��ǣ� ��
A. 11 B. 11��13 C. 13 D. ����ѡ�����ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������շѱ��ǣ���7Ԫ��ֻҪ��ʻ���벻����3km�����踶��7Ԫ��������3km����������1ǧ������2.4Ԫ������1km��1km���㣩���ִ�A�ص�B�ع�֧������19Ԫ����ô������ʻ�����·���ǣ� ��
A.9km
B.8km
C.7km
D.5km
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90�㣬BC��3 cm��AC��4 cm���Ե�CΪԲ�ģ���2.5 cmΪ�뾶��Բ�����C��ֱ��AB�к���λ�ù�ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016��������������ֵͻ��3000��Ԫ������3000���ÿ�ѧ��������ʾΪ�� ��
A.3��1012
B.30��1011
C.0.3��1011
D.3��1011
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com