
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ۢ� |
���� ���ݴ���ʽ�ı�ʾ�����ɶԢٽ����жϣ����ݶ��θ�ʽ������������ͷ�ʽ������������ɶԢڽ����жϣ��Ȱ�2xy-8x2y+8x3y��ʽ�ֽ⣬Ȼ�������������ķ������㣬��ɶԢ۽����жϣ����ݿ�ѧ�������Ķ���Ԣܽ����жϣ�
��� �⣺����ʽ$\frac{a}{b+1}$��������a����b��1�ĺͣ����Ԣٴ���
Ҫʹy=$\frac{\sqrt{3-x}}{x}$�����壬��xӦ������x��3��x��0�����Ԣڴ���
2xy-8x2y+8x3y=2xy��1-4x+4x2��=2xy��1-2x��2����2x-1=0ʱ��ԭʽ��ֵ��0�����Ԣ���ȷ��
�����ϵ�½�����ԼΪ149000000ƽ��ǧ�ף��ÿ�ѧ��������ʾΪ1.49��108ƽ��ǧ�ף����Ԣ���ȷ��
��ѡD��
���� ���⿼���������붨�����ж�һ���������䣬�������⣮�������ⶼ��������ͽ�����������ɣ���������֪�������������֪�����Ƴ������һ���������д�ɡ��������ô������ʽ�� ��Щ�������ȷ����������֤ʵ�ģ����������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�AD��BC�ڵ�D��BEƽ�֡�ABC������ABC=64�㣬��AEB=70�㣮
��ͼ����ABC�У�AD��BC�ڵ�D��BEƽ�֡�ABC������ABC=64�㣬��AEB=70�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
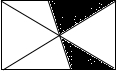 С������ͼ��ʾ�ľ���ֽ�����ǽ�ϣ��������Ϸ��ÿ�η��ھ�����ֽ���ϣ��������������Ӱ����ĸ����ǣ�������
С������ͼ��ʾ�ľ���ֽ�����ǽ�ϣ��������Ϸ��ÿ�η��ھ�����ֽ���ϣ��������������Ӱ����ĸ����ǣ�������| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
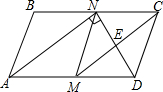 ��ͼ����ƽ���ı���ABCD�У�M��N�ֱ���AD��BC���е㣬��AND=90�㣬����CM��DN�ڵ�E��
��ͼ����ƽ���ı���ABCD�У�M��N�ֱ���AD��BC���е㣬��AND=90�㣬����CM��DN�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
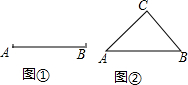 �����������һ���ϵ����߳�ǡ�õ�����ߵij�����ô�����������Ϊ�����������Ρ���
�����������һ���ϵ����߳�ǡ�õ�����ߵij�����ô�����������Ϊ�����������Ρ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{800}{x+50}$=$\frac{600}{x}$ | B�� | $\frac{800}{x-50}$=$\frac{600}{x}$ | C�� | $\frac{800}{x}$=$\frac{600}{x+50}$ | D�� | $\frac{800}{x}$=$\frac{600}{x-50}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3��-2�� | B�� | ��-3��2�� | C�� | ��3��-4�� | D�� | ��-3��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
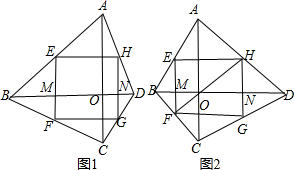
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com