
 如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.分析 (1)由角平分线得出∠EBC,得出∠BAD=26°,再求出∠C,即可得出∠CAD=52°;
(2)分两种情况:①当∠EFC=90°时;②当∠FEC=90°时;由角的互余关系和三角形的外角性质即可求出∠BEF的度数.
解答 (1)证明:∵BE平分∠ABC,
∴∠ABC=2∠EBC=64°,
∴∠EBC=32°,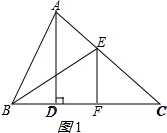
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠BAD=90°-64°=26°,
∵∠C=∠AEB-∠EBC=70°-32°=38°,
∴∠CAD=90°-38°=52°;
(2)解:分两种情况:
①当∠EFC=90°时,如图1所示: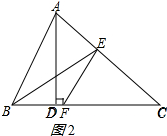
则∠BFE=90°,
∴∠BEF=90°-∠EBC=90°-32°=58°;
②当∠FEC=90°时,如图2所示:
则∠EFC=90°-38°=52°,
∴∠BEF=∠EFC-∠EBC=52°-32°=20°;
综上所述:∠BEF的度数为58°或20°.
点评 本题考查了三角形内角和定理、三角形的外角性质,角的互余关系;熟练掌握三角形内角和定理,并能进行推理论证与计算是解决问题的关键.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4(x+200-1)=5(x-1) | B. | 4(x+200)=5(x-1) | C. | 4(x+200-1)=5x | D. | 4(x+200)=5x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在2015年4月18日潍坊国际风筝节开幕上,小敏同学在公园广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.
在2015年4月18日潍坊国际风筝节开幕上,小敏同学在公园广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3•a4=a12 | B. | (2a)2•(-a)3=2a6 | C. | -(-a)2•(-a)3=a6 | D. | -(-a)2•a4=-a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
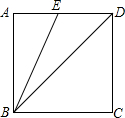 如图,已知正方形ABCD的边长为2,连接BD,BE平分∠ABD并交AD于点E,则DE的长是( )
如图,已知正方形ABCD的边长为2,连接BD,BE平分∠ABD并交AD于点E,则DE的长是( )| A. | 2 | B. | 2$\sqrt{2}$-2 | C. | 4-2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①④ | B. | ①② | C. | ②③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com