
【题目】甲乙两台智能机器人从同一地点出发,沿着笔直的路线行走了450cm.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.两机器人行走的路程y(cm)与时间x(s)之间的函数图像如图所示,根据图像所提供的信息解答下列问题: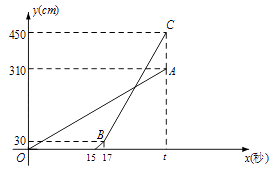
(1)乙比甲晚出发秒,乙提速前的速度是每秒cm, ![]() =;
=;
(2)已知甲匀速走完了全程,请补全甲的图象;
(3)当x为何值时,乙追上了甲?
【答案】
(1)15,15,31
(2)解:由图象可知,甲的速度为:310÷31=10(cm/s),
∴甲行走完全程450cm需 ![]() (s),函数图象如下:
(s),函数图象如下:
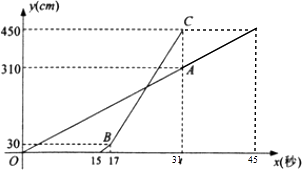
(3)解:设OA段对应的函数关系式为y=kx,
∵A(31,310)在OA上,
∴31k=310,解得k=10,
∴y=10x.
设BC段对应的函数关系式为y=k1x+b,
∵B(17,30)、C(31,450)在BC上,
∴ ![]() ,解得
,解得 ![]() ,
,
∴y=30x﹣480,
由乙追上了甲,得10x=30x﹣480,解得x=24.
答:当x为24秒时,乙追上了甲.
【解析】解:(1)由题意可知,当x=15时,y=0,故乙比甲晚出发15秒;
当x=15时,y=0;当x=17时,y=30;故乙提速前的速度是 ![]() (cm/s);
(cm/s);
∵乙出发一段时间后速度提高为原来的2倍,
∴乙提速后速度为30cm/s,
故提速后乙行走所用时间为: ![]() (s),
(s),
∴t=17+14=31(s);
所以答案是:(1)15,15,31.
【考点精析】通过灵活运用确定一次函数的表达式,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法即可以解答此题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
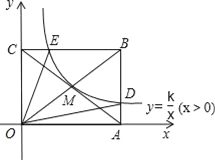
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称,过点A2作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称.过点A3作x轴的垂线,交直线y=2x于点B3;…按此规律作下去.则点A3的坐标为 , 点Bn的坐标为 . 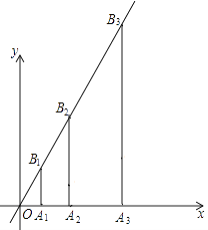
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中显示了10名同学平均每周用于阅读课外书的时间和用于看电视的时间(单位:小时)。
(1)用有序实数对表示图中各点。
(2)图中有一个点位于方格的对角线上,这表示什么意思?
(3)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列多项式应提取公因式5a2b的是( )
A.15a2b﹣20a2b2
B.30a2b3﹣15ab4﹣10a3b2
C.10a2b﹣20a2b3+50a4b
D.5a2b4﹣10a3b3+15a4b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边为( )
A. 3cm B. 7cm C. 7cm或3cm D. 7cm或5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程kx2﹣(3k﹣1)x+2(k﹣1)=0
(1)求证:无论k为任何实数,方程总有实数根;
(2)若此方程有两个实数根x1,x2,且|x1﹣x2|=2,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com