
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)经过A(﹣1,0),B(2,0)两点,与y轴交于点C.
(1)求抛物线的解析式及顶点D的坐标;
(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;
(3)点N在抛物线上,点M在抛物线的对称轴上,是否存在以点N为直角顶点的Rt△DNM与Rt△BOC相似?若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵抛物线y=ax2+bx﹣1(a≠0)经过A(﹣1,0),B(2,0)两点,
∴ ![]()
∴  ,
,
∴抛物线解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣1=
x﹣1= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∴抛物线的顶点坐标为( ![]() ,﹣
,﹣ ![]() )
)
(2)
解:如图1,

连接BC与抛物线对称轴的交点就是点P,连接AC,AP,
∵点A,B关于抛物线对称轴对称,
∴PA=PB,
∵B(2,0),C(0,﹣1),
∴直线BC解析式为y= ![]() x﹣1,
x﹣1,
∵点P在抛物线对称轴上,
∴点P的横坐标为 ![]() ,
,
∴点P的纵坐标为﹣ ![]() ,
,
∴P( ![]() ,﹣
,﹣ ![]() )
)
(3)
解:如图2,

过点作NF⊥DM,
∵B(2,0),C(0,﹣1),
∴OB=2,OC=1,
∴tan∠OBC= ![]() =
= ![]() ,tan∠OCB=
,tan∠OCB= ![]() =2,
=2,
设点N(m, ![]() m2﹣
m2﹣ ![]() m﹣1),
m﹣1),
∴FN=|m﹣ ![]() |,FD=|
|,FD=| ![]() m2﹣
m2﹣ ![]() m﹣1+
m﹣1+ ![]() |=|
|=| ![]() m2﹣
m2﹣ ![]() m+
m+ ![]() |,
|,
∵Rt△DNM与Rt△BOC相似,
∴∠MDN=∠OBC,或∠MDN=∠OCB,
①当∠MDN=∠OBC时,
∴tan∠MDN= ![]() =
= ![]() ,
,
∴ 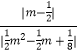 =
= ![]()
∴m= ![]() (舍)或m=
(舍)或m= ![]() 或m=﹣
或m=﹣ ![]() ,
,
∴N( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() ),
),
②当∠MDN=∠OCB时,
∴tan∠MDN= ![]() =2,
=2,
∴ 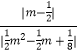 =2,
=2,
∴m= ![]() (舍)或m=
(舍)或m= ![]() 或m=﹣
或m=﹣ ![]() ,
,
∴N( ![]() ,﹣
,﹣ ![]() )或(﹣
)或(﹣ ![]() ,﹣
,﹣ ![]() );
);
∴符合条件的点N的坐标( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() )或(﹣
)或(﹣ ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)利用待定系数法求出抛物线解析式;(2)确定出当△ACP的周长最小时,点P就是BC和对称轴的交点,利用两点间的距离公式计算即可?(3)作出辅助线,利用tan∠MDN=2或 ![]() ,建立关于点N的横坐标的方程,求出即可.此题是二次函数综合题,主要考查了待定系数法,抛物线的对称性,三角函数,三角形周长的计算,绝对值方程,过点N作抛物线对称轴的垂线是解本题的关键也是难点.
,建立关于点N的横坐标的方程,求出即可.此题是二次函数综合题,主要考查了待定系数法,抛物线的对称性,三角函数,三角形周长的计算,绝对值方程,过点N作抛物线对称轴的垂线是解本题的关键也是难点.
【考点精析】本题主要考查了二次函数图象的平移和解直角三角形的相关知识点,需要掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,则PD等于( ) 
A.1
B.2
C.4
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究
问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
拓展
问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广
问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,小明购买一种笔记本所付款金额y(元)与购买量x(本)之间的函数图象由线段OB和射线BE组成,则一次购买8个笔记本比分8次购买每次购买1个可节省元. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年黔西南州教育局组织全州中小学生参加全省安全知识网络竞赛,在全州安全知识竞赛结束后,通过网上查询,某校一名班主任对本班成绩(成绩取整数,满分100分)作了统计分析,绘制成如下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题: 
(1)频数分布表中a= , b= , c=
(2)补全频数分布直方图
(3)为了激励学生增强安全意识,班主任准备从超过90分的学生中选2人介绍学习经验,那么取得100分的小亮和小华同时被选上的概率是多少?请用列表法或画树状图加以说明,并列出所有等可能结果.
频数分布表
分组(分) | 频数 | 频率 |
50<x 60 | 2 | 0.04 |
60<x 70 | 12 | a |
70<x<80 | b | 0.36 |
80<x 90 | 14 | 0.28 |
90<x 100 | c | 0.08 |
合计 | 50 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线n与过原点的直线m交于点P,P点的坐标如图所示,直线n与y轴交于点A;若OA=OP;
(1)求A点的坐标;
(2)求直线m,n的函数表达式;
(3)求△AOP的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com