
分析 (1)分别把点A(0,4),点B(1,0)代入二次函数y=x2+bx+c,求出b、c的值即可得出函数解析式;
(2)根据(1)中的函数解析式求出C、D两点的坐标,画出两函数在同一坐标系内的函数图象,根据函数的图象可得出结论.
解答 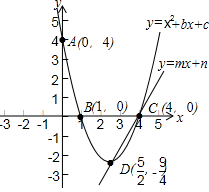 解:(1)∵二次函数y=x2+bx+c的图象与y轴交于点A(0,4),与x轴交于点B(1,0),
解:(1)∵二次函数y=x2+bx+c的图象与y轴交于点A(0,4),与x轴交于点B(1,0),
∴$\left\{\begin{array}{l}c=4\\ 1+b+c=0\end{array}\right.$,解得$\left\{\begin{array}{l}c=4\\ b=-5\end{array}\right.$,
∴二次函数的解析式为:y=x2-5x+4;
(2)∵y=x2-5x+4=(x-1)(x-4),
∴C(4,0).
∵当x=-$\frac{-5}{2}$=$\frac{5}{2}$时,y=$\frac{4×4-25}{4}$=-$\frac{9}{4}$,
∴D($\frac{5}{2}$,-$\frac{9}{4}$).
两函数图象如图所示,
由函数图象可知,当x<$\frac{5}{2}$或x>4时,x2+bx+c>mx+n.
点评 本题考查的是二次函数与不等式,根据题意画出函数图象,利用数形结合求解是解答此题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
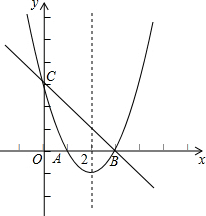 已知抛物线y=ax2+bx+3,与x轴交于A、B两点(如图),OB=OC=3OA,
已知抛物线y=ax2+bx+3,与x轴交于A、B两点(如图),OB=OC=3OA,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
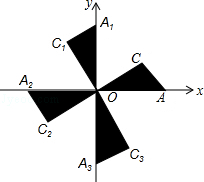 如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )| A. | 0 | B. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ | C. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2014}}$ | D. | $3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,已知直线AB的函数解析式为y=2x+10,与y轴交于点A,与x轴交于点B.
已知:如图,已知直线AB的函数解析式为y=2x+10,与y轴交于点A,与x轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
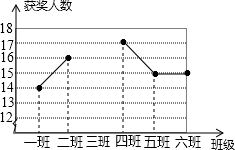 某中学组织网络安全知识竞赛活动,其中七年级6个班每班参赛人数相同,学校对该年级的获奖人数进行统计,得到平均每班获奖15人,并制作成如图所示不完整的折线统计图.
某中学组织网络安全知识竞赛活动,其中七年级6个班每班参赛人数相同,学校对该年级的获奖人数进行统计,得到平均每班获奖15人,并制作成如图所示不完整的折线统计图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com