
 已知:如图,已知直线AB的函数解析式为y=2x+10,与y轴交于点A,与x轴交于点B.
已知:如图,已知直线AB的函数解析式为y=2x+10,与y轴交于点A,与x轴交于点B.分析 (1)由直线AB解析式,令x=0与y=0分别求出y与x的值,即可确定出A与B的坐标;
(2)①把P坐标代入直线AB解析式,得到a与b的关系式,三角形POB面积等于OB为底边,P的纵坐标为高,表示出S与a的解析式即可;②存在,理由为:利用三个角为直角的四边形为矩形,得到四边形PFOE为矩形,利用矩形的对角线相等得到EF=PO,由O为定点,P为动点,得到OP垂直于AB时,OP取得最小值,利用面积法求出OP的长,即为EF的最小值.
解答  解:(1)对于直线AB解析式y=2x+10,
解:(1)对于直线AB解析式y=2x+10,
令x=0,得到y=10;令y=0,得到x=-5,
则A(0,10),B(-5,0);
(2)连接OP,如图所示,
①∵P(a,b)在线段AB上,
∴b=2a+10,
由0≤2a+10≤10,得到-5≤a≤0,
由(1)得:OB=5,
∴S△PBO=$\frac{1}{2}$OB•(2a+10),
则S=$\frac{5}{2}$(2a+10)=5a+25(-5≤a≤0);
②存在,理由为:
∵∠PFO=∠FOE=∠OEP=90°,
∴四边形PFOE为矩形,
∴EF=PO,
∵O为定点,P在线段AB上运动,
∴当OP⊥AB时,OP取得最小值,
∵$\frac{1}{2}$AB•OP=$\frac{1}{2}$OB•OA,
∴$\sqrt{{5}^{2}+1{0}^{2}}$•OP=50,
∴EF=OP=2$\sqrt{5}$,
综上,存在点P使得EF的值最小,最小值为2$\sqrt{5}$.
点评 此题属于一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,坐标与图形性质,矩形的判定与性质,勾股定理,以及三角形面积求法,熟练掌握性质及定理是解本题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 35.9×105平方米 | B. | 3.60×105平方米 | C. | 3.59×105平方米 | D. | 35.9×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
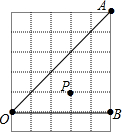 如图由边长为1cm正方形组成的6×5的方格阵,点O、A、B、P都在格点上〔即行和列的交点处),M、N分别是0A、OB上的动点,则△PMN周长的最小值是( )
如图由边长为1cm正方形组成的6×5的方格阵,点O、A、B、P都在格点上〔即行和列的交点处),M、N分别是0A、OB上的动点,则△PMN周长的最小值是( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 1+$\sqrt{2}$+$\sqrt{5}$ | D. | 2$+2\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动
某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动查看答案和解析>>
科目:初中数学 来源: 题型:填空题
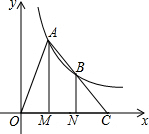 如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A,B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,且△BNC的面积为4,则k值为16.
如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A,B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,且△BNC的面积为4,则k值为16.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com