
| A. | $3\sqrt{5}-3$ | B. | $9-3\sqrt{5}$或$6-3\sqrt{5}$ | C. | $3\sqrt{5}-3$或$9-3\sqrt{5}$ | D. | $6-3\sqrt{5}$ |
分析 根据黄金分割点的定义,当AP是较长线段时,PA=$\frac{\sqrt{5}-1}{2}$AB;当AP是较短线段时,PA=$\frac{3-\sqrt{5}}{2}$AB,分别代入AB的值,进行计算即可得出答案.
解答 解:由于P为线段AB=6的黄金分割点,
当AP是较长线段时,PA=6×$\frac{\sqrt{5}-1}{2}$=3$\sqrt{5}$-3;
当AP是较短线段时,PA=6×$\frac{3-\sqrt{5}}{2}$=9-3$\sqrt{5}$;
故选C.
点评 此题考查了黄金分割,理解黄金分割点的概念.应该识记黄金分割的公式:较短的线段=原线段的$\frac{3-\sqrt{5}}{2}$,较长的线段=原线段的$\frac{\sqrt{5}-1}{2}$.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:选择题
| A. | (3,-2) | B. | (-3,2) | C. | (2,-3) | D. | (-2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
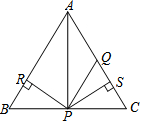 如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )
如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )| A. | ①②③④ | B. | ②③④ | C. | ①③④⑤ | D. | ①②③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 32,42,52 | B. | 1,$\sqrt{2}$,$\sqrt{3}$ | C. | 1,2,3 | D. | 12,22,32 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
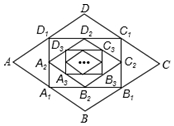 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A2nB2nC2nD2n的周长是( )
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A2nB2nC2nD2n的周长是( )| A. | $\frac{5}{{2}^{n-2}}$ | B. | $\frac{5}{{2}^{n-3}}$ | C. | $\frac{5}{{2}^{n}}$ | D. | $\frac{5}{{2}^{n-1}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com