
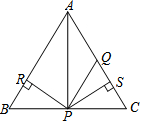
 如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )
如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )| A. | ①②③④ | B. | ②③④ | C. | ①③④⑤ | D. | ①②③⑤ |
分析 由三角形的面积可判断①正确;从而可知BP=PC,利用三腰三角形的性质可知AP为∠BAC的平分线,则可证得△ARP≌△ASP,可判断②;利用等腰三角形的性质和平行线的判定可判断③;由P为BC中点,PQ∥AB可知Q为AC中点,可判断⑤;由③正确可得到∠PQS=∠BAC,从而可判断④不正确;可得出答案.
解答 解:
∵AB=AC,PR=PS,PR⊥AB于点R,PS⊥AC于点S,
∴S△ABP=$\frac{1}{2}$AB•PR,S△ACP=$\frac{1}{2}$AC•PS,
∴S△ABP=S△ACP,故①正确;
∴BP=CP,
∴∠PAR=∠PAS,
在△APR和△APS中
$\left\{\begin{array}{l}{∠PAR=∠PAS}\\{∠ARP=∠ASP}\\{AP=AP}\end{array}\right.$
∴△APR≌△APS(AAS),
∴AR=AS,故②正确;
∵AQ=PQ,
∴∠PAQ=∠APQ=∠PAB,
∴PQ∥AB,故③正确;
∵P为BC中点,
∴Q为AC中点,
∴AQ=QC,故⑤正确;
若△BPR≌△QPS成立,则有∠PQS=∠B=∠BAC,则必有△ABC为等边三角形,而由题目条件无法得到,故④不正确;
综上可知正确的有①②③⑤,
故选D.
点评 本题主要考查等腰三角形的性质和全等三角形的判定和性质,由条件证得P点为BC的中点是解题的关键,注意等积法的运用.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{4}}$ | B. | $\sqrt{(-2)^{2}}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{-\frac{1}{4}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -42表示(-4)×(-4) | B. | -8没有立方根 | C. | $\sqrt{5}$与$-\sqrt{5}$是相反数 | D. | 64的平方根是8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $3\sqrt{5}-3$ | B. | $9-3\sqrt{5}$或$6-3\sqrt{5}$ | C. | $3\sqrt{5}-3$或$9-3\sqrt{5}$ | D. | $6-3\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
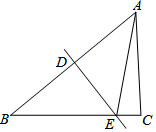 如图,在Rt△ABC中,∠ACB=90°,斜边AB的垂直平分线交AB于点D,交BC于点E.已知AB=5,AC=3,则△ACE的周长为( )
如图,在Rt△ABC中,∠ACB=90°,斜边AB的垂直平分线交AB于点D,交BC于点E.已知AB=5,AC=3,则△ACE的周长为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com