
【题目】如图,在ABCD中,AH∥CG,且分别交对角线BD于H、G,连接CH和AG,求证:∠CHG=∠AGH.

【答案】证明见解析.
【解析】
根据题意由AH∥CG得∠AHD=∠CGB,再由四边形ABCD是平行四边形知AD∥BC且AD=BC,据此得∠ADH=∠CBG,从而证△ADH≌△CBG得AH=CG,结合AH∥CG知四边形AHCG是平行四边形,继而得CH∥AG,由平行线的性质可得答案.
解:∵AH∥CG,
∴∠AHG=∠CGH,
∴180°﹣∠AHG=180°﹣∠CGH,即∠AHD=∠CGB.
∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∴∠ADH=∠CBG,
∴△ADH≌△CBG(AAS),
∴AH=CG,
∵AH∥CG,
∴四边形AHCG是平行四边形,
∴CH∥AG,
∴∠CHG=∠AGH.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】五一期间,小明随父母到某旅游胜地参观游览,他在游客中心O处测得景点A在其北偏东72°方向,测得景点B在其南偏东40°方向.小明从游客中心走了2千米到达景点A,已知景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果精确到0.1千米)
(参考数据:sin72°≈0.95,cos72°≈0.31,sin40°≈0.64,tan40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
(1)根据记录的数据可知该厂星期四生产自行车多少辆;
(2)根据记录的数据可知该厂本周实际生产自行车多少辆;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(0,a),B(0,b),C(m,b)且(a-4)2+![]() =0,
=0,![]()
(1)求C点坐标
(2)作DE DC,交y轴于E点,EF为 AED的平分线,且DFE= 90o。 求证:FD平分ADO;
(3)E 在 y 轴负半轴上运动时,连 EC,点 P 为 AC 延长线上一点,EM 平分∠AEC,且 PM⊥EM,PN⊥x 轴于 N 点,PQ 平分∠APN,交 x 轴于 Q 点,则 E 在运动过程中,![]() 的大小是否发生变化,若不变,求出其值.
的大小是否发生变化,若不变,求出其值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某建筑物AC上,挂着一宣传条幅BC,站在点F处,测得条幅顶端B的仰角为300,往条幅方向前行20米到达点E处,测得条幅顶端B的仰角为600,求宣传条幅BC的长.(![]() ,结果精确到0.1米)
,结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 重合),延长
重合),延长![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)填空:
①当![]() 的值为_______时,四边形
的值为_______时,四边形![]() 是矩形;
是矩形;
②当![]() 的值为______时,四边形
的值为______时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
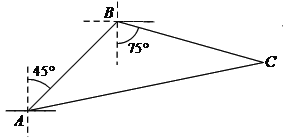
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一副直角三角板(角度分别为30°、60°、90°和45°、45°、90°),如图(1)所示,其中一块三角板的直角边AC垂直于数轴,AC的中点过数轴原点O,AC=8,斜边AB交数轴于点G,点G对应数轴上的数是4;另一块三角板的直角边AE交数轴于点F,斜边AD交数轴于点H.
(1)如果△AGH的面积是10,△AHF的面积是8,则点F对应的数轴上的数是 ,点H对应的数轴上的数是 ;
(2)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,若∠HAO=a,试用a来表示∠M的大小:(写出推理过程)
(3)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,设∠EFH的平分线和
∠FOC的平分线交于点N,求∠N+∠M的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.求:

(1)转动转盘,转出的数字大于3的概率是多少?
(2)现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.这三条线段能构成三角形的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com