
【题目】(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积.
(3)拓展提升:如图3,等边△EBC中,EC=BC=4cm,点O在BC上,且OC=3cm,动点P从点E沿射线EC以2cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间ts.

【答案】(1)详见解析;(2)18;(3)2.5秒.
【解析】
(1)利用同角的余角相等判断出∠CAE=∠BCD,即可得出结论;
(2)先作出高,进而判断出△ABC≌△B'AG,求出B'G,最后用三角形的面积公式即可得出结论;
(3)利用等式的性质得出,∠CPO=∠BOF,进而判断出△BOF≌△PCO,即可求出CP=1,即可得出结论.
(1)∵BD⊥l,AE⊥l,
∴∠AEC=∠CDB=90°,
∴∠CAE+∠ACE=90°,
∵∠ACB=90°,
∴∠ACE+∠BCD=90°,
∴∠CAE=∠BCD,
在△ACE和△CBD中,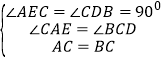 ,
,
∴△ACE≌△CBD;
(2)如图2,过点B'作B'G⊥AC于G,
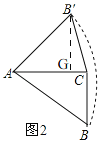
∴∠B'AG+∠AB'G=90°,
∵∠BAB'=90°,
∴∠BAC+∠B'AG=90°,
∴∠AB'G=∠BAC,由旋转知,AB=AB',
在△ABC和△B'AG中,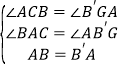 ,
,
∴△ABC≌△B'AG,
∴B'G=AC=6,
∴S△ACB'=![]() AC×B'G=18;
AC×B'G=18;
(3)如图3,
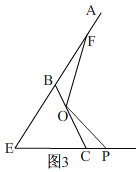
由旋转知,OP=OF,
∵△BCE是等边三角形,
∴∠CBE=∠BCE=60°,
∴∠OCP=∠FBO=120°,∠CPO+∠COP=60°,
∵∠POF=120°,
∴∠COP+∠BOF=60°,
∴∠CPO=∠BOF,
在△BOF和△PCO中,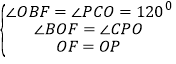 ,
,
∴△BOF≌△PCO,
∴CP=OB,
∵EC=BC=4cm,OC=3cm,
∴OB=BC﹣OC=1,
∴CP=1,
∴EP=CE+CP=5,
∴点P运动的时间t=5÷2=2.5秒.


科目:初中数学 来源: 题型:
【题目】如图,AC是正方形ABCD的对角线,将△ACD绕着点A顺时针旋转后得到△AC′D′,点D′落在AC上,C′D′交BC于点E,若AB=1,则图中阴影部分图形的面积是 . 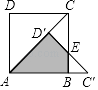
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4). 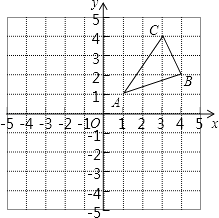
(1)①请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②请画出△ABC关于原点对称的△A2B2C2;
(2)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
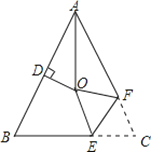
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC= 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
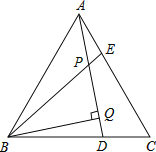
【题目】如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q.
(1)求证:△ADC≌△BEA;
(2)若PQ=4,PE=1,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边三角形ABC的边长为12,点P为AC上一点,点D在CB的延长线上,且BD=AP,连接PD交AB于点E,PE⊥AB于点F,则线段EF的长为( )

A. 6 B. 5
C. 4.5 D. 与AP的长度有关
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上. 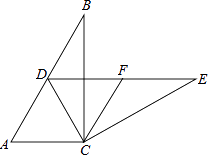
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=﹣2x2+1,下列说法错误的是( )
A.图象开口向下
B.图象的对称轴为x= ![]()
C.函数最大值为1
D.当x>1时,y随x的增大而减小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com