
����Ŀ��ͼ1��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ֳ��Ŀ�С�����Σ�Ȼ��ͼ2����״ƴ��һ�������Σ�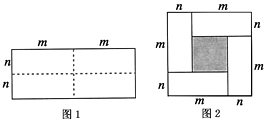
��1���������ֲ�ͬ�ķ�����ͼ2����Ӱ���ֵ������
����1����
����2����
��2���۲�ͼ2����д��������������ʽ����m+n��2 �� ��m-n��2 �� mn֮��ĵ�����ϵ��
��3�����ݣ�2�����еĵ�����ϵ������������⣺
����֪�� ![]() ��
�� ![]() ����
���� ![]() ��ֵ��
��ֵ��
����֪�� ![]() ��
�� ![]() ����
���� ![]() ��ֵ.
��ֵ.
���𰸡�
��1����m��n��2,��m+n��2��4mn
��2����m��n��2����m+n��2��4mn����m��n��2=��m+n��2��4mn
��3���⣺��a��b=5��ab=��6��
�ࣨa+b��2=��a��b��2+4ab=52+4������6��=25��24=1��
�ڽ⣺����֪�ã���a+ ![]() ��2=��a��
��2=��a�� ![]() ��2+4a
��2+4a ![]() =12+8=9��
=12+8=9��
��a��0��a+ ![]() ��0��
��0��
��a+ ![]() =3
=3
���������⣺��1������1����m��n��2��
����2����m+n��2��4mn��
�� 2 ����m��n��2=��m+n��2��4mn��
���Դ��ǣ���m��n��2����m+n��2��4mn����m��n��2=��m+n��2��4mn��


 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���������㣬����һ���ǵ����߷ֱ�����һ���ǵ����ߵ�_______����������λ�ù�ϵ�������ǻ�Ϊ�Զ��ǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ1����A���߶�DE��һ�㣬��BAC=90�㣬AB=AC��BD��DE��CE��DE�� 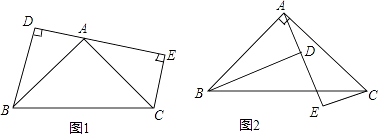
��1����֤��DE=BD+CE��
��2���������ͼ2���ͼ�Σ������ܵõ�ʲô���ۣ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ǡ�ABC������ABC=40�㣬��ACB=70�㣬��D��E�ڱ�AB��AC�ϣ�CD��BE���ڵ�H��
��1����BE��AC��CD��AB�����BHC�Ķ�����
��2����BE��CDƽ�֡�ABC�͡�ACB�����BHC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�������εĶ��㴦�ֱ������1, 2, 3, 4,5, 6,�ܷ�ʹ�����������ڶ��㴦��������֮��
��1������9?
��2������10?����,����ͼ�б����;������,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��EF��AD����1=��2, ��BAC=70�㣬�����AGD�Ĺ������������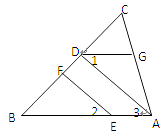
�⣺��EF��AD
���2=����
�֡ߡ�1=��2
���1=��3����
��AB������
�ߡ�BAC+=180�㣨��
�ߡ�BAC=70�� ���AGD=��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
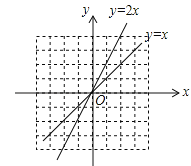
����Ŀ����ͼ���Ѻ���y=x��ͼ���ϸ�����������Ϊԭ����2���������겻�䣬�õ�����y=2x��ͼ��Ҳ���Ѻ���y=x��ͼ���ϸ���ĺ������Ϊԭ����![]() ���������겻�䣬�õ�����y=2x��ͼ��
���������겻�䣬�õ�����y=2x��ͼ��
���Ƶأ����ǿ�����ʶ����������
��1���Ѻ���![]() ��ͼ���ϸ�����������Ϊԭ���� ���������겻�䣬�õ�����
��ͼ���ϸ�����������Ϊԭ���� ���������겻�䣬�õ�����![]() ��ͼ��Ҳ���Ѻ���
��ͼ��Ҳ���Ѻ���![]() ��ͼ���ϸ���ĺ������Ϊԭ���� ���������겻�䣬�õ�����
��ͼ���ϸ���ĺ������Ϊԭ���� ���������겻�䣬�õ�����![]() ��ͼ��
��ͼ��
��2����֪���б仯��������ƽ��2����λ���ȣ�������ƽ��1����λ���ȣ�������ƽ��![]() ����λ���ȣ����������Ϊԭ����4���������겻�䣻�ݺ������Ϊԭ����
����λ���ȣ����������Ϊԭ����4���������겻�䣻�ݺ������Ϊԭ����![]() ���������겻�䣻�������Ϊԭ����2���������겻�䣮
���������겻�䣻�������Ϊԭ����2���������겻�䣮
������![]() ��ͼ�������еĵ㾭���ܡ��ڡ��٣��õ����� ��ͼ��
��ͼ�������еĵ㾭���ܡ��ڡ��٣��õ����� ��ͼ��
����Ϊ�˵õ�����![]() ��ͼ���Ѻ���
��ͼ���Ѻ���![]() ��ͼ�������еĵ� ��
��ͼ�������еĵ� ��
A���١��ݡ���B���١��ޡ���C���١��ڡ���D���١��ۡ���
��3������![]() ��ͼ����Ծ��������ı仯�õ�����
��ͼ����Ծ��������ı仯�õ�����![]() ��ͼ��д��һ�ּ��ɣ�
��ͼ��д��һ�ּ��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Ӳ�Ʒ����11�¡�12���������ν��ۣ��ۼ���3900Ԫ������2500Ԫ����ƽ��ÿ�½��۵İٷ���Ϊx�����������г��ķ����ǣ�������
A. 3900��1+x��2=2500 B. 3900��1��x��2=2500
C. 3900��1��2x��=2500 D. 2500��1+x��2=3900
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com