
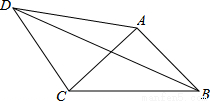
如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
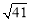 .
.
【解析】
试题分析:根据等式的性质,可得∠BAD与∠CAD′的关系,根据SAS,可得△BAD与△CAD′的关系,根据全等三角形的性质,可得BD与CD′的关系,根据勾股定理,可得答案:
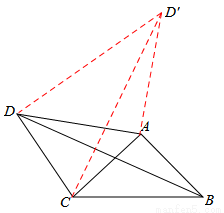
如答图,作AD′⊥AD,AD′=AD,连接CD′,DD′,
∵∠ABC=∠ACB=45°,∴BA=BC.
∵∠BAC+∠CAD=∠DAD′+∠CAD,即∠BAD=∠CAD′,
在△BAD与△CAD′中,∵ ,∴△BAD≌△CAD′(SAS).∴BD=CD′.
,∴△BAD≌△CAD′(SAS).∴BD=CD′.
在Rt△ADD′中,由勾股定理得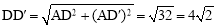 .
.
∵∠D′DA=∠ADC=45°,∴∠D′DC=90°.
在Rt△CDD′中,由勾股定理得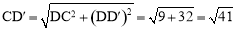 ,
,
∴BD=CD′=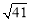 .
.
考点:1.等腰直角三角形的判定和性质;2.全等三角形的判定和性质;3.勾股定理;4.转换思想的应用.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源:2014年初中毕业升学考试(湖南常德卷)数学(解析版) 题型:填空题
古生物学家发现350 000 000年前,地球上每年大约是400天,用科学记数法表示350 000 000= .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南娄底卷)数学(解析版) 题型:填空题
如图,?ABCD的对角线AC、BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南娄底卷)数学(解析版) 题型:选择题
函数 y= 中自变量x的取值范围为( )
中自变量x的取值范围为( )
A.x≥0 B.x≥﹣2 C.x≥2 D.x≤﹣2
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北武汉卷)数学(解析版) 题型:解答题
袋中装有大小相同的2个红球和2个绿球,
(1)先从袋中摸出1个球后放回,混合均匀后再摸出1个球,
① 求第一次摸到绿球,第二次摸到红球的概率;
② 求两次摸到的球中有1个绿球和1个红球的概率;
(2)先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是多少?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北武汉卷)数学(解析版) 题型:选择题
在一次中学生田径运动会上,参加调高的15名运动员的成绩如下表所示:
成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
那么这些运动员跳高成绩的众数是( )
A.4 B.1.75 C.1.70 D.1.65
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:选择题
要使分式 有意义,则的取值范围是( )
有意义,则的取值范围是( )
A. x≠1 B. x>1 C. x<1 D. x≠﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com