练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．若三角形的三边长分别为a、b、c，满足a2b-a2c+b2c-b3=0，这个三角形是（　　）
    A．等腰三角形B．直角三角形
    C．等边三角形D．三角形的形状不确定

    分析 首先将原式变形为a2（b-c）+b2（c-b）=0，就有（b-c）（a2-b2）=0，可以得到b-c=0或a-b=0或a+b=0，进而得到b=c或a=b．从而得出△ABC的形状．

    解答 解：∵a2b-a2c+b2c-b3=0，
    ∴a2（b-c）+b2（c-b）=0，
    ∴（b-c）（a2-b2）=0，
    （b-c）（a-b）（a+b）=0，
    ∴b-c=0或a-b=0或a+b=0（舍去），
    ∴△ABC是等腰三角形．
    故选A．

    点评 本题考查因式分解提公因式法在实际问题中的运用，等腰三角形的判定和直角三角形的判定．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．已知抛物线y=ax2+bx+c（a≠0）与x轴交点为（-1，0）和（3，0），与y轴交点为（0，-2），则一元二次方程ax2+bx+c=0（a≠0）的根为（　　）
    A．x1=-1，x2=3B．x1=-2，x2=3C．x1=1，x2=-3D．x1=-1，x2=-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

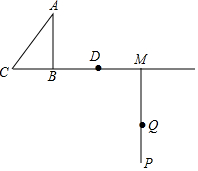    14．如图，Rt△ABC中，∠ABC=90°，AB=4，BC=3，点D从B点出发，沿射线CB方向以每秒3个单位长度的速度运动，射线MP⊥射线CB，且BM=10，点Q从M点出发，沿射线MQ方向以每秒a个单位长度的速度运动，己知D，Q两点同时出发，记时间为t．
    （1）当t=10时，△DMQ是等腰三角形，求a的值；
    （2）求t为何值时，△DCA为等腰三角形；
    （3）若△DMQ与△ABC全等，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．在实数$\sqrt{2}$，π，$\frac{3}{7}$，-$\root{3}{8}$，2.1616…，2.1010010001…（每两个1之间依次多1个0）中，无理数有（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．已知a、b互为相反数，m、n互为倒数，且m不等于1，-1，x的绝对值为2，计算-2mn+$\frac{a+b}{m-n}$-x2=-6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．据不完全统计，2016年国庆期间来北京旅游的人数达700000人，用科学记数法可表示700000为（　　）
    A．0.7×105B．0.7×106C．7×105D．7×106

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．一个口袋中有6个黑球和若干个白现球，从口袋中随机摸出一球，记下其颜色，再把它放回去，不断重复上述过程，共摸了200次，其中有51次摸到黑球，则据此估计口袋中大约有白球18个．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年江苏省无锡市八年级3月月考数学试卷（解析版） 题型：填空题

    如图，在平面直角坐标系中，点A的坐标为(1，1)，OA＝AC，∠OAC＝90°，点D为x轴上一动点，以AD为边在AD的右侧作正方形ADEF．

    (1)如图(1)当点D在线段OC上时（不与点O、C重合），则线段CF与OD之间的数量关系为 ；位置关系为 ．

    (2)如图(2)当点D在线段OC的延长线上时，(1)中的结论是否成立？若成立，请说明理由；若不成立，请举一反例；

    (3)设D点坐标为(t，0)，当D点从O点运动到C点时，用含t的代数式表示E点坐标，并直接写出E点所经过的路径长．

    查看答案和解析>>

    科目：初中数学 来源：2017届江苏省九年级下学期第一次月考数学试卷（解析版） 题型：单选题

    如图，正方形ABCD的边长为4cm，动点P、Q同时从点A出发，以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动，设运动时间为x(单位：s)，四边形PBDQ的面积为y(单位：cm2)，则y与x(0≤x≤8)之间的函数关系可用图象表示为 ( )

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案