
| A. | x1=-1,x2=3 | B. | x1=-2,x2=3 | C. | x1=1,x2=-3 | D. | x1=-1,x2=-2 |
分析 根据抛物线与x轴的交点问题,两交点的横坐标即为方程ax2+bx+c=0的解.
解答 解:∵抛物线y=ax2+bx+c与x轴的两个交点分别为(-1,0),(3,0),
即自变量为-1和3时函数值为0,
∴一元二次方程ax2+bx+c=0的根为x1=-1,x2=3.
故选A.
点评 本题考查了抛物线与x轴的交点,关键是掌握求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


科目:初中数学 来源: 题型:选择题
 如图,OP是∠AOB的平分线,点C、D分别在∠AOB的两边OA、OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
如图,OP是∠AOB的平分线,点C、D分别在∠AOB的两边OA、OB上,添加下列条件,不能判定△POC≌△POD的选项是( )| A. | ∠OPC=∠OPD | B. | PC=PD | C. | PC⊥OA,PD⊥OB | D. | OC=OD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )| A. | 40cm | B. | 6cm | C. | 8cm | D. | 10cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
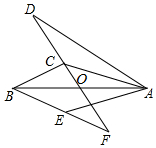 如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )
如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等边三角形 | D. | 三角形的形状不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com