
【题目】(1)叙述三角形中位线定理,并运用平行四边形的知识证明;
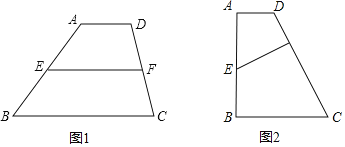
(2)运用三角形中位线的知识解决如下问题:如图1,在四边形ABCD中,AD∥BC,E、F分别是AB,CD的中点,求证:EF=![]() (AD+BC)
(AD+BC)
(3)如图2,在四边形ABCD中,AD∥BC,∠B=900,AD=3,BC=4,CD=7,E是AB的中点,直接写出点E到CD的距离.
【答案】(1)详见解析;(2)详见解析;(3)2![]() .
.
【解析】
(1)作出图形,写出已知、求证,延长EF到D,使FD=EF,证明△AEF≌△CDF,根据全等三角形对应边相等可得AE=CD,全等三角形对应角相等可得∠D=∠AEF,再求出CE=CD,根据内错角相等,两直线平行判断出AB∥CD,然后判断出四边形BCDE是平行四边形,根据平行四边形的性质可得DE∥BC,DE=BC;
(2)连接AF并延长,交BC延长线于点M,根据ASA证明△ADF≌△MCF,判断EF是△ABM的中位线,根据三角形中位线定理即可得出结论;
(3)作DN⊥BC于N,连接DE并延长交CB的延长线于H,连接EC,证明CH=CD,根据等腰三角形的三线合一得到∠ECH=∠ECD,根据角平分线的性质解答即可.
(1)三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半;
已知:△ABC中,点E、F分别是AB、AC的中点,
求证:EF∥BC,EF=![]() BC,
BC,
证明:如图,延长EF到D,使FD=EF,如图所示:
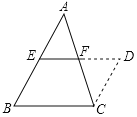
∵点F是AC的中点,
∴AF=CF,
在△AEF和△CDF中,
 ,
,
∴△AEF≌△CDF(SAS),
∴AE=CD,∠D=∠AEF,
∴AB∥CD,
∵点E是AB的中点,
∴AE=BE,
∴BE=CD,
∴四边形BCDE是平行四边形,
∴DE∥BC,DE=BC,
∴DE∥BC,EF=![]() BC;
BC;
(2)证明:连接AF并延长,交BC延长线于点M,如图所示:
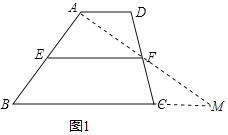
∵AD∥BC,
∴∠D=∠FCM,
∵F是CD中点,
∴DF=CF,
在△ADF和△MCF中,
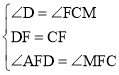 ,
,
∴△ADF≌△MCF(ASA)
∴AF=FM,AD=CM,
∴EF是△ABM的中位线,
∴EF∥BC∥AD,EF=![]() BM=
BM=![]() (AD+BC);
(AD+BC);
(3)解:作DN⊥BC于N,
则四边形ABND为矩形,
∴AB=DN,BN=AD=3,
∴NC=1,
∴DN=![]() =4
=4![]() ,
,
∴EB=![]() AB=
AB=![]() DN=2
DN=2![]() ,
,
连接DE并延长交CB的延长线于H,连接EC,如图所示:
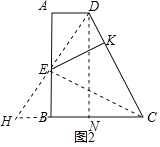
∵E是AB的中点,
∴BH=AD=3,DE=EH,
∴CH=CB+BH=7,
∴CD=CH,又DE=EH,
∴∠ECH=∠ECD,EB⊥BC,EK⊥CD,
∴EK=EB=2![]() .
.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:
如果一个三角形的三边长分别为a,b,c,记p=![]() ,那么这个三角形的面积S=
,那么这个三角形的面积S=![]() .这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式。中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦---九韶公式”完成下列问题:
.这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式。中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦---九韶公式”完成下列问题:
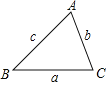
如图,在△ABC中,a=7,b=5,c=6.
(1)求△ABC的面积;
(2)设AB边上的高为h1,AC边上的高为h2,求h1 +h2的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前,安徽黄山脚下的小村庄的集市上,人山人海,还有人在摆“摸彩”游戏,只见他手拿一个黑色的袋子,内装大小、形状、质量完全相同的白球20只,且每一个球上都写有号码(1~20号)和1只红球,规定:每次只摸一只球.摸前交1元钱且在1~20内写一个号码,摸到红球奖5元,摸到号码数与你写的号码相同奖10元.
(1)你认为该游戏对“摸彩”者有利吗?说明你的理由.
(2)若一个“摸彩”者多次摸奖后,他平均每次将获利或损失多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
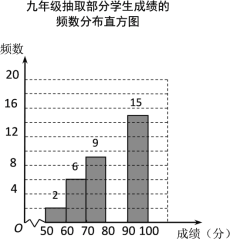
【题目】某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
![]()
成绩x/分 | 频数 | 频率 | |
第1段 | x<60 | 2 | 0.04 |
第2段 | 60≤x<70 | 6 | 0.12 |
第3段 | 70≤x<80 | 9 | b |
第4段 | 80≤x<90 | a | 0.36 |
第5段 | 90≤x≤100 | 15 | 0.30 |
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)样本中,部分学生成绩的中位数落在第_______段;
(4)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=![]() S△BOC,求点D的坐标.
S△BOC,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
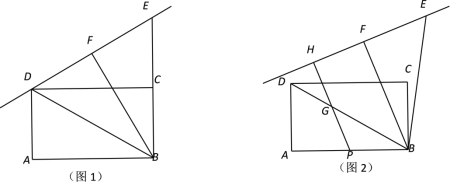
【题目】已知,在矩形ABCD中,BC=2,连接BD,把△ABD绕点B顺时针旋转后得到△FBE,旋转角度小于360°.
(1)如图1,当点E在BC的延长线上,且直线EF过点D,求AB的长.
(2)若AB=4,如图2,取AB边的中点P,过点P作直线EF的垂线PH,垂足为H.
① 若PH交线段BD于点G,当△BPG为等腰三角形时,求BG的长;
② 直接写出PH长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,点P在∠AOB的内部,P1与P关于OA对称,P2与P关于OB对称,则△P1OP2是
A. 含30°角的直角三角形 B. 顶角是30的等腰三角形
C. 等边三角形 D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
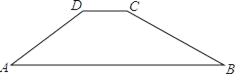
【题目】如图所示,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,斜坡AD=8m,斜坡BC的坡度i=1:3,B,C间的水平距离为12m,则斜坡AD的坡角∠A=_____,坝底宽AB=______m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两色的正方形瓷砖铺设长方形地面,观察下列图形并解答问题.
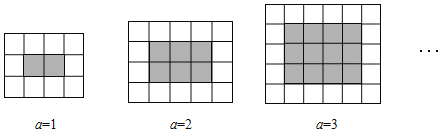
(1)在第a个图中,共有 块白瓷砖和 块黑瓷砖(用含a的代数式表示);
(2)若按上图的方式铺一块长方形地面共用了420块瓷砖,求此时a的值;
(3)已知白瓷砖每块6元,黑瓷砖每块8元,某工厂按如图方式铺设厂房地面,其中黑瓷砖的费用比白瓷砖的费用多924元,问白瓷砖和黑瓷砖各用了多少块?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com