
����Ŀ����ͼ����ͬ�����ĺڰ���ɫ�������δ�ש���賤���ε��棬�۲�����ͼ�β�������⣮
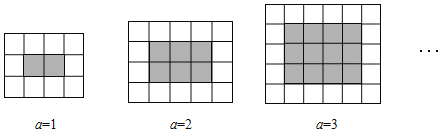
��1���ڵ�a��ͼ�У������� ����״�ש���� ����ڴ�ש���ú�a�Ĵ���ʽ��ʾ����
��2��������ͼ�ķ�ʽ��һ�鳤���ε��湲����420���ש�����ʱa��ֵ��
��3����֪�״�שÿ��6Ԫ���ڴ�שÿ��8Ԫ��ij��������ͼ��ʽ���賧�����棬���кڴ�ש�ķ��ñȰ״�ש�ķ��ö�924Ԫ���ʰ״�ש�ͺڴ�ש�����˶��ٿ飿
���𰸡���1��4a+6��a��a+1������2��18����3���״�ש�ͺڴ�ש�ֱ�����54��156�飮
��������
��1�����ȹ۲�ͼ�Σ����ݵ�a��ͼ�εĺڴ�ש��ÿ���У�a+1������ÿ����a�����ڴ�ש������Ϊa��a+1����Ȼ����ݺ��к����еĴ�ש������������ɵó��״�ש�Ŀ�����
��2������ͼ���г����̽�ü��ɣ�
��3���ɣ�1���ó��������úڴ�ש�Ͱ״�ש�ķ��ã�Ȼ���������г����̣���ü���.
��1�����ݵ�a��ͼ�εĺڴ�ש��ÿ���У�a+1������ÿ����a�����ڴ�ש������Ϊa��a+1����
��ͼ��ÿһ������a+3���ש��ÿһ������a+2���ש�������ܿ���Ϊ��a+2����a+3����
��״�ש����Ϊ����a+2����a+3����a��a+1����4a+6��
�ʴ�Ϊ��4a+6��a��a+1����
��2�����ͼ���ã���a+2����a+3����420��
��ã�a1��18��a2����23������������ȥ��
�ఴͼ�ķ�ʽ��һ�鳤���ε��湲����420���שʱa��ֵΪ18��
��3���ɣ�1���ã��������úڴ�ש�ķ���Ϊ8a��a+1��Ԫ���״�ש�ķ���Ϊ6��4a+6��Ԫ��
������ã�8a��a+1����6��4a+6����924
��ã�a1��12��a2����10������������ȥ��
�ڴ�ש������a��a+1����156��
�״�ש������4a+6��54��
�𣺰״�ש�ͺڴ�ש�ֱ�����54��156�飮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��������������λ�߶�����������ƽ���ı��ε�֪ʶ֤����
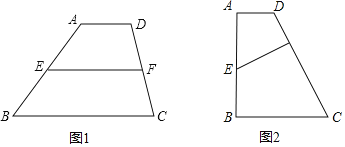
��2��������������λ�ߵ�֪ʶ����������⣺��ͼ1�����ı���ABCD�У�AD��BC��E��F�ֱ���AB��CD���е㣬��֤��EF��![]() ��AD+BC��
��AD+BC��
��3����ͼ2�����ı���ABCD�У�AD��BC����B��900��AD��3��BC��4��CD��7��E��AB���е㣬ֱ��д����E��CD�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Rt��ABC������AC=6cm��BC=8cm��AB=10cm����AB���ϵ�����Ϊ_____cm��AB���ϵĸ�Ϊ_____cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
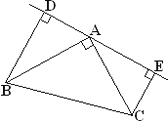
����Ŀ����ͼ(1), ��֪��ABC��, ��BAC=900, AB=AC, AE�ǹ�A��һ��ֱ��, ��B��C��A��E�����, BD��AE��D, CE��AE��E
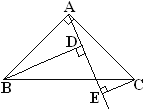
��1����˵��: BD=DE+CE.
��2����ֱ��AE��A����ת��ͼ(2)λ��ʱ(BD<CE), ������������, ��BD��DE��CE�Ĺ�ϵ���? Ϊʲô��
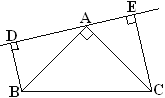
��3����ֱ��AE��A����ת��ͼ(3)λ��ʱ(BD>CE), ������������, ��BD��DE��CE�Ĺ�ϵ���? �� ֱ��д�����, ����˵��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�E��BC���е㣬����AE���ӳ���DC���ӳ����ڵ�F��

��1����֤��AB=CF��
��2������DE����AD=2AB����֤��DE��AF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ҵ�ˣ����꼶![]() ��ͬѧ��֯��һ�ξۻ����Լ������ǵ����꣮��ͬѧ����ȥҰ��۲ͣ���ͬѧ����ȫ��һ��ȥ��һ����Ӱ��Ҳ��ͬѧϣ����չһ��������������ᣮ�����ʽ��ʱ�����⣬������������ֻ�ܲ������������ͬѧ�Ǿ�����ǩ��������ȫ���
��ͬѧ��֯��һ�ξۻ����Լ������ǵ����꣮��ͬѧ����ȥҰ��۲ͣ���ͬѧ����ȫ��һ��ȥ��һ����Ӱ��Ҳ��ͬѧϣ����չһ��������������ᣮ�����ʽ��ʱ�����⣬������������ֻ�ܲ������������ͬѧ�Ǿ�����ǩ��������ȫ���![]() ��ͬѧ������ǩ��һ��������ǩ��ǩ�Ϸֱ����
��ͬѧ������ǩ��һ��������ǩ��ǩ�Ϸֱ����![]() ��
��![]() ��
��![]() ������ĸ��
������ĸ��![]() ����Ұ��۲ͣ�
����Ұ��۲ͣ�![]() ��������Ӱ��
��������Ӱ��![]() �����������ᣬÿ��ͬѧ������ǩ���³�ȡ��ǩȻ��Żأ����������г鵽������������������Ļ������ξۻ�Ļ��Ŀ�ֱ���Ұ��۲ͺͿ�չ������ĸ����ǣ� ��
�����������ᣬÿ��ͬѧ������ǩ���³�ȡ��ǩȻ��Żأ����������г鵽������������������Ļ������ξۻ�Ļ��Ŀ�ֱ���Ұ��۲ͺͿ�չ������ĸ����ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�ټ����ض�ͯ������ڣ����ϰ��мס����������ӣ�ÿ����ʢ�а���2������ɳ��1��������1�������������ȫһ������
��1��С���Ӽ�������ȡһ�����ӣ�ȡ����ɳ�յĸ����� ��
��2��С���ڼ��̺��������Ⱥ��ȡ��һ�����ӣ�������״ͼ���б�����С��ǡ��ȡ�����������ӵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B��C������ֱ�Ϊ��-1,3������-4,1����(-2,1)���Ƚ���ABC��һȷ������ƽ�Ƶõ���A![]() B
B![]() C
C![]() ����B�Ķ�Ӧ��B
����B�Ķ�Ӧ��B![]() ��������(1,2)���ٽ���A
��������(1,2)���ٽ���A![]() B
B![]() C
C![]() ��ԭ��O˳ʱ����ת90��õ���A
��ԭ��O˳ʱ����ת90��õ���A![]() B
B![]() C
C![]() ,��A
,��A![]() �Ķ�Ӧ��Ϊ��A
�Ķ�Ӧ��Ϊ��A![]() .
.
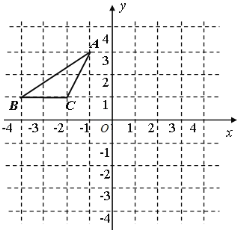
(1) ������A![]() B
B![]() C
C![]() ��
�� ![]()
(2) ������A![]() B
B![]() C
C![]() ��
��
(3) ����������α任�����У���A������A![]() �����A
�����A![]() ��·���ܳ�.
��·���ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
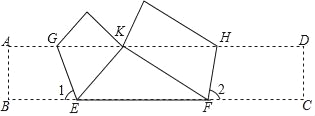
����Ŀ����ͼ��������ABCD��ֽƬ���۵���ʹ��B��AD���ϵĵ�K�غϣ�EGΪ�ۺۣ���C��AD���ϵĵ�K�غϣ�FHΪ�ۺۣ���֪��1=67.5�㣬��2=75�㣬EF=![]() +1����BC�ij���
+1����BC�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com