(1)证明:∵四边形ABCD是平行四边形
∴AD∥BC,OA=OC,
在△EAO和△FCO中,

,
从而可得△EAO≌△FCO,
故可得AE=CF;
(2)解:当点E运动到使AE=3.2时,四边形AECF是矩形.理由如下:
∵四边形AECF是矩形,
∴△ACE和△DCE都是直角三角形,
根据勾股定理得,EC
2=AC
2-AE
2,EC
2=DC
2-DE
2,
∴AC
2-AE
2=DC
2-DE
2,即4
2-a
2=3
2-(5-a)
2,
解得:a=3.2;
(3)解:当点E运动到AE中点时,四边形AECF是菱形;理由如下:
∵E是AE中点,
∴DE=AE=FC=2.5.
∵AD∥BC,
∴四边形EFCD和四边形AECF都是平行四边形,
∴EF∥CD,
由已知CD=3,CA=4,CB=5,
∴AD
2=AC
2+CD
2,得出∠ACD=90°,
∴∠AOE=∠ACD=90°,
∴四边形AECF是菱形.
分析:(1)根据平行四边形的性质,得出OA=OC,继而结合平行线的性质可判断△EAO≌△FCO,从而证得结论.
(2)根据四边形AECF是矩形,可得出△ACE和△DCE都是直角三角形,继而利用勾股定理表示出DE
2,建立方程可得出答案.
(3)先判断出四边形EFCD和四边形AECF都是平行四边形,然后得出∠AOE=∠ACD=90°,从而根据菱形的判定即可得出结论.
点评:此题考查了平行四边形的性质、勾股定理、菱形的判定及矩形的性质,综合考察的知识点较多,解答本题关键是要求所学知识的融会贯通.

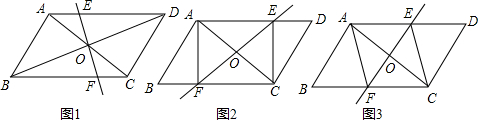
 ,
,

 次方程x2-7x+12=0的两个根,且OA>OB.
次方程x2-7x+12=0的两个根,且OA>OB.
