
【题目】如图:AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有( ) 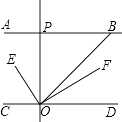
A.①②③④
B.①②③
C.①③④
D.①②④
【答案】B
【解析】解:①∵AB∥CD,
∴∠BOD=∠ABO=40°,
∴∠COB=180°﹣40°=140°,
又∵OE平分∠BOC,
∴∠BOE= ![]() ∠COB=
∠COB= ![]() ×140°=70°.(故①正确)
×140°=70°.(故①正确)
②∵OP⊥CD,
∴∠POD=90°,
又∵AB∥CD,
∴∠BPO=90°,
又∵∠ABO=40°,
∴∠POB=90°﹣40°=50°,
∴∠BOF=∠POF﹣∠POB=70°﹣50°=20°,
∠FOD=40°﹣20°=20°,
∴OF平分∠BOD.(故②正确)
③∵∠EOB=70°,∠POB=90°﹣40°=50°,
∴∠POE=70°﹣50°=20°,
又∵∠BOF=∠POF﹣∠POB=70°﹣50°=20°,
∴∠POE=∠BOF.(故③正确)
④由②可知∠POB=90°﹣40°=50°,
∠FOD=40°﹣20°=20°,
故∠POB≠2∠DOF.(故④错误)
故选:B.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对平行线的性质的理解,了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点P( ![]() x+1,3x﹣8)的横、纵坐标恰好为某个正数的两个平方根.
x+1,3x﹣8)的横、纵坐标恰好为某个正数的两个平方根. 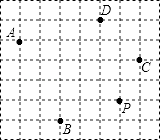
(1)求点P的坐标;
(2)在图中建立平面直角坐标系,并分别写出点A,B,C,D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,点E在直线AB,CD之间. 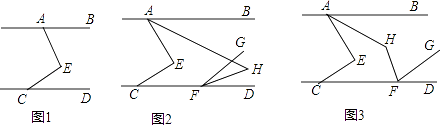
(1)求证:∠AEC=∠BAE+∠ECD;
(2)若AH平分∠BAE,将线段CE沿CD平移至FG.
①如图2,若∠AEC=90°,HF平分∠DFG,求∠AHF的度数;
②如图3,若HF平分∠CFG,试判断∠AHF与∠AEC的数量关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
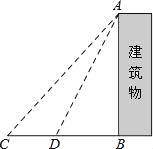
【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈![]() ,tan48°≈
,tan48°≈![]() ,sin64°≈
,sin64°≈![]() ,tan64°≈2)
,tan64°≈2)
查看答案和解析>>
科目:初中数学 来源: 题型:
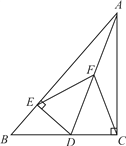
【题目】如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连结EF、CF.
(1)若AD平分∠BAC,求证:EF=CF.
(2)若点F是线段AD的中点,试猜想线段EF与CF的大小关系,并加以证明.
(3)在(2)的条件下,若∠BAC=45°,AD=6,直接写出C、E两点间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com