
【题目】如图,已知AB∥CD,点E在直线AB,CD之间. 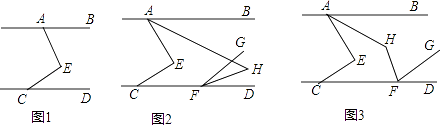
(1)求证:∠AEC=∠BAE+∠ECD;
(2)若AH平分∠BAE,将线段CE沿CD平移至FG.
①如图2,若∠AEC=90°,HF平分∠DFG,求∠AHF的度数;
②如图3,若HF平分∠CFG,试判断∠AHF与∠AEC的数量关系并说明理由.
【答案】
(1)解:如图1,过点E作直线EN∥AB,
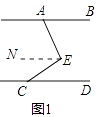
∵AB∥CD,
∴EN∥CD,
∴∠BAE=∠AEN,∠DCE=∠CEN,
∴∠AEC=∠AEN+∠CEN=∠BAH+∠ECD
(2)解:∵AH平分∠BAE,
∴∠BAH=∠EAH,
①∵HF平分∠DFG,设∠GFH=∠DFH=x,
又CE∥FG,
∴∠ECD=∠GFD=2x,
又∠AEC=∠BAE+∠ECD,∠AEC=90°,
∴∠BAH=∠EAH=45°﹣x,
如图2,过点H作l∥AB,
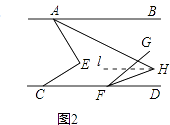
易证∠AHF=∠BAH+∠DFH=45°﹣x+x=45°;
②设∠GFD=2x,∠BAH=∠EAH=y,
∵HF平分∠CFG,
∴∠GFH=∠CFH=90°﹣x,
由(1)知∠AEC=∠BAE+∠ECD=2x+2y,
如图3,过点H作l∥AB,
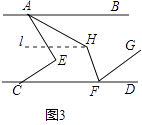
易证∠AHF﹣y+∠CFH=180°,
即∠AHF﹣y+90°﹣x=180°,∠AHF=90°+(x+y),
∴∠AHF=90°+ ![]() ∠AEC.(或2∠AHF﹣∠AEC=180°.)
∠AEC.(或2∠AHF﹣∠AEC=180°.)
【解析】(1)过E作EF∥AB,可得∠A=∠AEF,利用平行于同一条直线的两直线平行得到EF与CD平行,再得到一对内错角相等,进而得出答案;(2)①HF平分∠DFG,设∠GFH=∠DFH=x,根据平行线的性质可以得到∠AHF的度数;②设∠GFD=2x,∠BAH=∠EAH=y,根据角平分线的性质以及平行线的性质即可得到∠AHF与∠AEC的数量关系.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补),还要掌握平移的性质(①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1, ![]() ),将线段OA平移至线段BC,B(3,0).
),将线段OA平移至线段BC,B(3,0).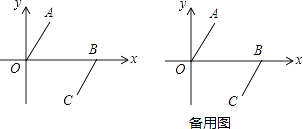
(1)请直接写出点C的坐标;
(2)连AC,AB,求三角形ABC的面积;
(3)若∠AOB=60°,点P为y轴上一动点(点P不与原点重合),试探究∠CPO与∠BCP之间的数量关系并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有( ) 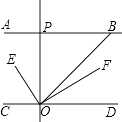
A.①②③④
B.①②③
C.①③④
D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别是边AB、AC的中点,将△ADE沿着DE对折,点A落在BC边上的点F,若∠B=50°,则∠BDF的度数为( ) 
A.50°
B.70°
C.75°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪计划中考后参加“我的中国梦”夏令营活动,需要一名家长陪同,爸爸、妈妈用猜拳的方式确定由谁陪同,即爸爸、妈妈随机做出“石头”、 “剪刀”“布” 三种手势中的一种,规定:“石头”胜“剪刀”,“剪刀” 胜“布”,“布” 胜“石头”,手势相同,不分胜负.
(1)爸爸一次出“石头”的概率是多少?
(2)妈妈一次获胜的概率是多少?请用列表或画树状图的方法加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com