
【题目】如图,点A(1, ![]() ),将线段OA平移至线段BC,B(3,0).
),将线段OA平移至线段BC,B(3,0).
(1)请直接写出点C的坐标;
(2)连AC,AB,求三角形ABC的面积;
(3)若∠AOB=60°,点P为y轴上一动点(点P不与原点重合),试探究∠CPO与∠BCP之间的数量关系并证明你的结论.
【答案】
(1)
解:如图,
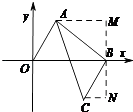
∵点A(1, ![]() ),将线段OA平移至线段BC,B(3,0).
),将线段OA平移至线段BC,B(3,0).
∴BM=BN= ![]() ,
,
∴C(2,﹣ ![]() )
)
(2)
解:连接OC,
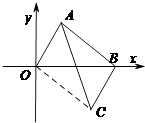
∵B(3,0)
∴OB=3,
由平移得,四边形OABC是矩形,
S三角形ABC=S三角形OBC= ![]() OB×|yC|=
OB×|yC|= ![]() ×3×
×3× ![]() =
= ![]()
(3)
解:过点P作直线l∥AO,
∵OA∥BC,
∴l∥BC,
①如图,
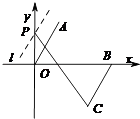
当点P在y轴负半轴时,BC与y轴交点(含交点)上方时.
∠CPO+∠BCP=360°﹣90°﹣60°=210°
②如图,
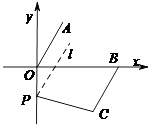
当点P在y轴负半轴时,BC与y轴交点(含交点)下方时.
∠BCP﹣∠CPO=150°
③当点P在y轴正半轴时,
∠BCP﹣∠CPO=∠AOy=90°﹣60°=30°
【解析】(1)由平移得到BM=BN= ![]() ,从而得出点C坐标;(2)由平移得到四边形OABC是矩形,△ABC的面积和△OAB的面积一样大,(3)分三种情况讨论计算,①当点P在y轴负半轴时,BC与y轴交点(含交点)上方时.②当点P在y轴负半轴时,BC与y轴交点(含交点)下方时,③当点P在y轴正半轴时,简单计算即可.
,从而得出点C坐标;(2)由平移得到四边形OABC是矩形,△ABC的面积和△OAB的面积一样大,(3)分三种情况讨论计算,①当点P在y轴负半轴时,BC与y轴交点(含交点)上方时.②当点P在y轴负半轴时,BC与y轴交点(含交点)下方时,③当点P在y轴正半轴时,简单计算即可.
【考点精析】关于本题考查的图形的平移和平移的性质,需要了解对应线段,对应点所连线段平行(或在同一直线上)且相等;对应角相等;平移方向和距离是它的两要素;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】某码头上有20名工人装载一批货物,已知每人往一艘轮船上装载2吨货物,装载完毕恰好用了6天,轮船到达目的地后,另一批工人开始卸货,计划平均每天卸货v吨,刚要卸货时遇到紧急情况,要求船上的货物卸载完毕不超过4天,则这批工人实际每天至少应卸货( )
A. 30吨 B. 40吨 C. 50吨 D. 60吨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC. 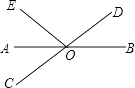
(1)若∠EOC=72°,求∠BOD的度数;
(2)若∠DOE=2∠AOC,判断射线OE,OD的位置关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某校冬季运动会上,有15名选手参加了200米预赛,取前八名进入决赛.已知参赛选手成绩各不相同,某选手要想知道自己是否进入决赛,除了知道自己的成绩外,还需要了解全部成绩的( )
A. 平均数 B. 中位数 C. 众数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,点E在直线AB,CD之间. 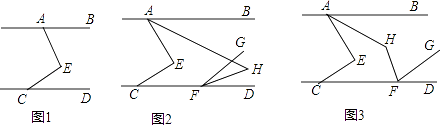
(1)求证:∠AEC=∠BAE+∠ECD;
(2)若AH平分∠BAE,将线段CE沿CD平移至FG.
①如图2,若∠AEC=90°,HF平分∠DFG,求∠AHF的度数;
②如图3,若HF平分∠CFG,试判断∠AHF与∠AEC的数量关系并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com