
 如图所示,当小明站立在镜子EF前A处时,他看自己的脚在镜中的像的俯角为45°;如果小华向后退0.6米到B处,这时他看自己的脚在镜中的像的俯角为30°.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据:
如图所示,当小明站立在镜子EF前A处时,他看自己的脚在镜中的像的俯角为45°;如果小华向后退0.6米到B处,这时他看自己的脚在镜中的像的俯角为30°.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据:| 3 |
| AC |
| AA1 |
| BD |
| BB1 |
| AC |
| AA1 |
| BD |
| BB1 |
| 3 |
| 3 |


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
 如图,△ABC内接于⊙O,AB=AC,过点A作BC的平行线与BO的延长线交于点P.
如图,△ABC内接于⊙O,AB=AC,过点A作BC的平行线与BO的延长线交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,二次函数y=ax2+4的图象与x轴交于点A和点B(点A在点B 的左侧),与y轴交于点C,且cos∠CAO=
已知:如图,二次函数y=ax2+4的图象与x轴交于点A和点B(点A在点B 的左侧),与y轴交于点C,且cos∠CAO=
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,二次函数y=ax2-
如图,二次函数y=ax2-| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图由等腰直角三角形组成,其中第一个直角三角形的腰长为1cm,
如图由等腰直角三角形组成,其中第一个直角三角形的腰长为1cm,查看答案和解析>>
科目:初中数学 来源: 题型:
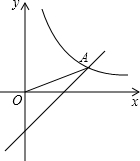 已知:在平面直角坐标系xOy中,直线y=x-4k与双曲线y=
已知:在平面直角坐标系xOy中,直线y=x-4k与双曲线y=| 16k |
| x |
| 3 |
| 16k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com