
 如图,二次函数y=ax2-
如图,二次函数y=ax2-| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
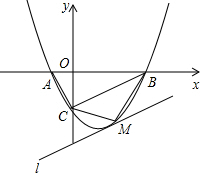 解:(1)将A(-1,0)、点C(0,-2).代入y=ax2-
解:(1)将A(-1,0)、点C(0,-2).代入y=ax2-| 3 |
| 2 |
|
|
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |

| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
|
|
|
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
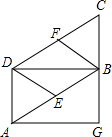 已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点.
已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,当小明站立在镜子EF前A处时,他看自己的脚在镜中的像的俯角为45°;如果小华向后退0.6米到B处,这时他看自己的脚在镜中的像的俯角为30°.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据:
如图所示,当小明站立在镜子EF前A处时,他看自己的脚在镜中的像的俯角为45°;如果小华向后退0.6米到B处,这时他看自己的脚在镜中的像的俯角为30°.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据:| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下:| 等第 人数 类别 | A | B | C | D |
| 农村 | 200 | 240 | 80 | |
| 县镇 | 290 | 132 | 130 | |
| 城市 | 240 | 132 | 48 |
查看答案和解析>>
科目:初中数学 来源: 题型:
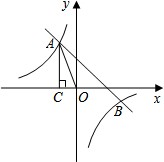 如图,直线y=ax+b与双曲线y=
如图,直线y=ax+b与双曲线y=| k |
| x |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 | ||
2+
|
| 1 |
| 2 |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com