
分析 先判断出三角形中必有一个内角为2°,再根据三角形的内角和质数的意义列举出即可.
解答 解:∵三个内角的和是180°,是一个偶数,
∴必有一个内角为偶数,
又∵三角形三个内角的度数都是质数,
∴既是偶数又是质数的只有2;
∴这三个内角中必定有一个内角等于2°;
①2°,5°,173°;
②2°,11°,167°;
③2°,29°,149°;
④2°,41°,137°;
⑤2°,47°,131°,
⑥2°,71°,107°;
⑦2°,89°,89°.
故答案为:2°,5°,173°; 2°,11°,167°; 2°,29°,149°; 2°,41°,137°; 2°,47°,131°;2°,71°,107°; 2°,89°,89°共7种.
点评 此题考查了三角形的内角和定理,三个质数的和是偶数中必有一个既是质数又是偶数的数只有2,得出既是质数又是偶数的数只有2是解本题的关键.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:选择题
| A. | 110° | B. | 35° | C. | 140° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
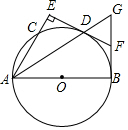 如图△ABG中,∠ABG=90°,以AB为直径作⊙O交于D点,D是弧BC的中点,过D作AC的垂线,垂足为E,ED的延长线交BG于F.
如图△ABG中,∠ABG=90°,以AB为直径作⊙O交于D点,D是弧BC的中点,过D作AC的垂线,垂足为E,ED的延长线交BG于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
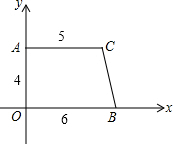 如图,在直角梯形AOBC中,AC平行于OB,且OB=6,AC=5,OA=4,
如图,在直角梯形AOBC中,AC平行于OB,且OB=6,AC=5,OA=4,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
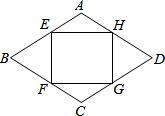 如图,在菱形ABCD的边上依次取点E,F,G,H,使AE=AH=CF=CG,若菱长边长是1,∠A=120°,
如图,在菱形ABCD的边上依次取点E,F,G,H,使AE=AH=CF=CG,若菱长边长是1,∠A=120°,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com