
ij���糧����6̨��������磬ÿ̨�ķ�����Ϊ300��ǧ��/�£��ó��ƻ��ӽ���7�¿�ʼ����ף���6̨�����������һ�θ���������ÿ�¸�������1̨����̨���������ͣ�������ڴ�����Ͷ�뷢�磬ÿ̨���������������ÿ�µķ���������ԭ�����20%����֪ÿ̨��������������ķ���Ϊ20��Ԫ��������7�·���Ϊ��1���¿�ʼ�����㣬�ó���x��x�������������µķ�������Ϊy����ǧ�ߣ���
��1����ó���2���µķ������������°�����ܷ�������
��2����y����x�ĺ�����ϵʽ��
��3�����ÿ��1ǧ�ߵ����ӯ��0.04Ԫ����ô�ӵ�1���¿�ʼ������Ҫ���ڼ����£����ڼ�ó��ķ���ӯ���۳�����������������ú��ӯ���ܶ��1����Ԫ����������ͬ��ʱ���ڷ����������������ʱ�ķ���ӯ���ܶ��2����Ԫ����
��1��1560ǧ�ߣ�9900ǧ������2��y=60x+1440��1��x��6������3��17.
��������
�����������1�����������֪����1���µķ�������300��5ǧ�ߣ���2���µķ�����Ϊ300��4+300��1+20%������3���µķ�����Ϊ300��3+300��2����1+20%������4���µķ�����Ϊ300��2+300��3����1+20%������5���µķ�����Ϊ300��1+300��4����1+20%������6���µķ�����Ϊ300��5����1+20%������6���µ��ܵ����������Ϳ�������ܵ�����
��2�����ܷ�����=��̨�����ķ�����֮���ݣ�1���Ľ�����y��x֮��Ĺ�ϵʽΪy=kx+b���������������⼴��.
��3����������=����ӯ��������������������ã��ֱ��ʾ����1����2���ٸ���������������ʽ���
��⼴�ɣ�
�����������������
��1�������⣬��
��2���µķ�����Ϊ��300��4+300��1+20%��=1560ǧ�ߣ�
�����°�����ܷ�����Ϊ��
300��5+1560+300��3+300��2����1+20%��+300��2+300��3����1+20%��+300��1+300��4����1+20%��+300��5����1+20%��
=1500+1560+1620+1680+1740+1800=9900��
�𣺸ó���2���µķ�����Ϊ1560ǧ�ߣ������°�����ܷ�����Ϊ9900ǧ��.
��2����y��x֮��Ĺ�ϵʽΪy=kx+b�������⣬��
 ����ã�
����ã� .
.
��y����x�ĺ�����ϵʽΪy=60x+1440��1��x��6����
��3���赽��n����ʱ��1����2��
��n=6ʱ����1=9900��0.04��20��6=276����2=300��6��6��0.04=432����1����2�����ϣ�
��n��6��
����1=[9900+360��6��n��6��]��0.04��20��6=86.4n��240����2=300��6n��0.04=72n��
����1����2ʱ��86.4n��240��72n����֮��n��16.7����n=17��
������Ҫ����17���¦�1������2��
���㣺1.һ�κ����Ͳ���ʽ��Ӧ�ã�2.��ʵ�������к�����ϵʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ����ջ���������ѧ�������棩 ���ͣ������
��ͼ1������OABC����B������Ϊ��8��3��������D������Ϊ��12��0��������P�ӵ�O��������ÿ��2����λ���ȵ��ٶ���x��������������˶�������Q�ӵ�D��������ÿ��1����λ���ȵ��ٶ���x��ĸ����������˶���PQ����ͬʱ�˶�������ʱֹͣ�����˶������У���PQΪб����x���Ϸ�������ֱ��������PQR�����˶�ʱ��Ϊt�룮
��1����t=�� ��ʱ����PQR�ı�QR������B��
��2�����PQR�;���OABC�ص����ֵ����ΪS����S����t�ĺ�����ϵʽ��
��3����ͼ2��������E��5��0����EF��BC������ΪF������PQR�Ķ���R���ھ���OABC���ڲ�ʱ������R��x�ᡢy���ƽ���ߣ��ֱ�EF��BC�ڵ�M��N������MAN=45�㣬��t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ����ջ���������ѧ�������棩 ���ͣ������
��һ�����������߳��ֱ�Ϊ2��3��x����x��ֵ����Ϊ�� ����ֻ����һ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ����ջ���������ѧ�������棩 ���ͣ�ѡ����
С��ͬѧij������Ŀ7�β��Գɼ����£���λ���֣���9��7��10��8��10��9��10���������ݵ���λ���������ֱ�Ϊ��������
A��8��10 B��10��9 C��8��9 D��9��10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ���������������ѧ�������棩 ���ͣ������
��ͼ��AB�ǰ�ԲO��ֱ����C��D�ǰ�ԲO�ϵ����㣬��OD��BC��OD��AC���ڵ�E��
��1������B=70�㣬����CAD�Ķ�����
��2����AB=4��AC=3����DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ���������������ѧ�������棩 ���ͣ������
��ͼ����֪��P�ǰ뾶Ϊ1����A��һ�㣬�ӳ�AP��C��ʹPC=AP����ACΪ�Խ����� ABCD����AB=
ABCD����AB=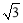 ����
���� ABCD��������ֵΪ ��
ABCD��������ֵΪ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������ݾ�����ѧ�������棩 ���ͣ������
��ͼ������ABCD�ı�AB=3cm��AD=4cm����E�ӵ�A������������AD�ƶ�����CEΪֱ����ԲO����FΪԲO������BD�Ĺ����㣬����EF��CF������E��EG��EF��EG��ԲO�ཻ�ڵ�G������CG��
��1����˵���ı���EFCG�Ǿ��Σ�
��2����ԲO������BD����ʱ����Eֹͣ�ƶ����ڵ�E�ƶ��Ĺ����У�
������EFCG������Ƿ�������ֵ����Сֵ�������ڣ����������ֵ����Сֵ���������ڣ�˵�����ɣ�
�����G�ƶ�·�ߵij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com