
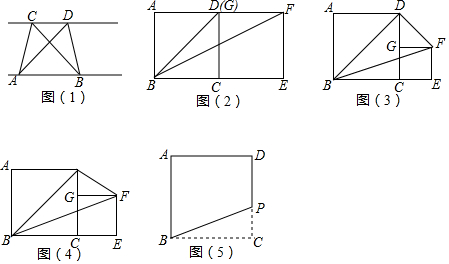
分析 (1)(2)(3)连接FC,∠BDC=∠DCF=45°,根据内错角相等,两直线平行可以证明BD∥CF,然后根据题目信息可以得到:△BDF的面积=△ABD的面积;
探索应用:同理,连接BD,过点C作BD的平行线,交BP的延长线于点M,则:△BDM的面积=△BDC的面积,所以补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BP上.
解答  解:(1)18,
解:(1)18,
(2)18,
(3)18,
理由如下:连接CF,
∵BD、CF分别为两正方形的对角线,
∴∠BDC=∠DCF=45°,
∴BD∥CF,
∴S△BDF=S△CBD=18;
探索应用:连接BD,过C点作BD的平行线交BP的延长线于M,连接DM,
则S△BDM=S△CBD,
∴S△BDM-S△BDP=S△CBD-S△BDP,
即:S△DMP=S△PCB.
∴补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BP上.
点评 本题考查了信息获取能力及四边形的综合知识,读懂题目信息,构造出平行线是利用三角形面积相等进行转化求解三角形的面积的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
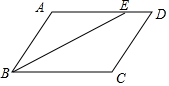 如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于E,∠AEB=25°,则∠A的大小为( )
如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于E,∠AEB=25°,则∠A的大小为( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0)、B(3,6)、C(10,8)、D(13,0),确定这个四边形的面积.
如图,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0)、B(3,6)、C(10,8)、D(13,0),确定这个四边形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
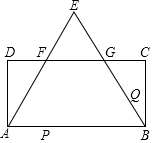 矩形ABCD中,AB=CD=18cm,以AB为边向上作正△ABE,AE、BE分别交CD于F、G,DF=5cm,两动点P、Q运动速度分别为4cm/s、v(cm/s).
矩形ABCD中,AB=CD=18cm,以AB为边向上作正△ABE,AE、BE分别交CD于F、G,DF=5cm,两动点P、Q运动速度分别为4cm/s、v(cm/s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com