
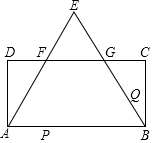
 矩形ABCD中,AB=CD=18cm,以AB为边向上作正△ABE,AE、BE分别交CD于F、G,DF=5cm,两动点P、Q运动速度分别为4cm/s、v(cm/s).
矩形ABCD中,AB=CD=18cm,以AB为边向上作正△ABE,AE、BE分别交CD于F、G,DF=5cm,两动点P、Q运动速度分别为4cm/s、v(cm/s).分析 (1)由矩形的性质和等边三角形的性质即可得出答案;
(2)由全等三角形的性质得出相等的线段,得出方程,解方程即可;注意讨论;
(3)分两种情况讨论,根据路程、时间、速度关系进行分析解答.
解答 (1)解:∵四边形ABCD是矩形,△ABE是等边三角形,
∴AB∥CD,AE=AB=18cm,
由对称性得:CG=DF=5cm,
∴FG=CD-DF-CG=8cm,AF=10cm,
∴EF=FG=8cm,
∴AF=AE-EF=10cm,
故答案为:10;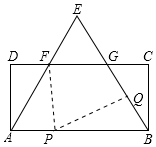
(2)解:又题意得:AP=4t,PB=18-4t,
①当△AFP≌△BPQ时,PB=AF,
即:18-4t=10,
∴t=2s,
此时:AP=4t=8cm=BQ,
2V=8,
∴V=4cm\s
②当△AFP≌△BQP时,AF=BQ,AP=PB,
即:4t=18-4t 解得:t=$\frac{9}{4}$s,
∵$\frac{9}{4}$V=10,∴V=$\frac{40}{9}$cm/s,
(3)解:①当Q的速度为V=4cm\s时,因为点P的速度也为4cm\s∴P,Q不会相遇
②当点Q的速度为V=$\frac{40}{9}$cm/s时,
∵$\frac{40}{9}$cm/s>4cm/s,
∴点Q能追上点P
设:追上的时间为xs.
又∵P,Q沿逆时针运动,Q、P距离为28cm
根据题意得:$\frac{40}{9}$x-4x=28,
解得:x=63,
又∵P的速度为4cm\s,
∴P运动63s共走了:4×63=252cm
而P从A出发逆时针,沿四边形ABGF的边运动,转一圈为46cm
∵46×5+22=252cm,
∴P在沿四边形ABGF的边逆时针运动了5圈又运动了22cm后在BG边距点B 4cm处与点Q相遇(或距离点G6cm处与点Q相遇).
点评 本题是四边形综合题目,考查了矩形的性质、全等三角形的性质、路程、时间、速度关系等知识;本题综合性强,有一定难度.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
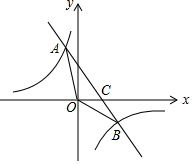 如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于第二、四象限内的A、B两点,与x轴交于点C,点A的坐标为(-3,n),线段OB=10,且sin∠BOC=$\frac{3}{5}$.
如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于第二、四象限内的A、B两点,与x轴交于点C,点A的坐标为(-3,n),线段OB=10,且sin∠BOC=$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠ABC=∠BCD
如图,∠ABC=∠BCD查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.求证:
如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com