
| 3 |
| 4 |
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 到A村庄 | 到B村庄 | |
| C城市 | 每吨15元 | 每吨12元 |
| D城市 | 每吨10元 | 每吨9元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
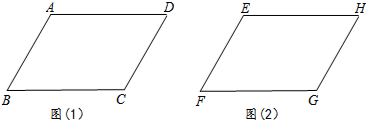
查看答案和解析>>
科目:初中数学 来源: 题型:
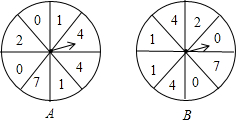 北京时间2014年6月30日凌晨,来自巴西和德国的球迷Oscar和Kroos利用“争1点”的游戏来预测2014年巴西世界杯冠军,如图两个可以自由转动的转移A、B,每个转盘被分成8个相等的扇形,其规则如下:
北京时间2014年6月30日凌晨,来自巴西和德国的球迷Oscar和Kroos利用“争1点”的游戏来预测2014年巴西世界杯冠军,如图两个可以自由转动的转移A、B,每个转盘被分成8个相等的扇形,其规则如下:查看答案和解析>>
科目:初中数学 来源: 题型:
| (-2)2 |
| 1 |
| 2 |
| 2a+2 |
| a-1 |
| a2-1 |
| a2-2a+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com