
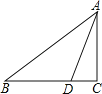
【题目】如图,Rt△ABC中,∠C=90°,BD=4,CD=2,∠ADB=3∠ABD,则AD= .
【答案】![]() .
.
【解析】
试题分析:如图,作BD的垂直平分线,交AB于点E,连接DE,设∠ABD=α,证明∠AED=∠ADE=2α,AE=AD;证明AE=2BE(设为2λ),得到AD=AE=2λ;利用勾股定理,可证明4λ2﹣4=9λ2﹣36,解得:λ=![]() ,求出AD即可解决问题.
,求出AD即可解决问题.
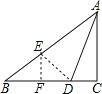
解:如图,作BD的垂直平分线,交AB于点E,连接DE,设∠ABD=α,设BE=λ,
则BE=DE=λ,BF=DF=2,CF=4;
∴∠ABD=∠EDB=α;
∵∠AED=∠ABD+∠EDB=2α,∠ADB=3∠ABD=3α,
∴∠AED=∠ADE=2α,AE=AD;
∵EF⊥BC,AC⊥BC,
∴EF∥AC,![]() =
=![]() =2,
=2,
∴AE=2BE=2λ,
∴AD=AE=2λ;
由勾股定理得:
AC2=AD2﹣DC2=4λ2﹣4,
AC2=AB2﹣BC2=9λ2﹣36,
∴4λ2﹣4=9λ2﹣36,
解得:λ=![]() ,
,
∴AD=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC、CD于点M、F,BG⊥AC,垂足为G,BG交AE于点H。
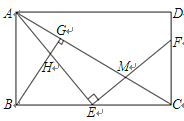
(1)求证:△ABE∽△ECF;
(2)找出与△ABH相似的三角形,并证明;
(3)若E是BC中点,BC=2AB,AB=2,求EM的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
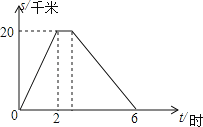
【题目】在一条笔直的公路上,依次有A、C、B三地.小明从A地途经C地前往距A地20千米的B地,到B地休息一段时间后立即按原路返回到A地.小明出发4小时的时候距离A地12千米.小明去时从C地到B地,返回时再由B地到C地(包括在B地休息的时间)共用2小时.他与A地的距离s(单位:千米)和所用的时间t(单位:小时)之间的函数关系如图所示.下列说法:①小明去时的速度为10千米/时;②小明在B地休息了![]() 小时;③小明回来时的速度为6千米/时;④C地与A地的距离为15千米,其中正确的个数为( )
小时;③小明回来时的速度为6千米/时;④C地与A地的距离为15千米,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】移动互联网已经全面进入人们的日常生活,截止2016年5月,全国4G用户总数达到11.2亿,其中11.2亿用科学记数法表示为( )
A. 11.2×108 B. 112×107 C. 1.12×109 D. 1.12×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解我校八年级同学的视力情况,从八年级的15个班共590名学生中,每班随机抽取了5名进行分析。在这个问题中.样本是____________________,样本容量是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且![]() ,四边形DCFE是平行四边形,则图中阴影部分的面积为( ).
,四边形DCFE是平行四边形,则图中阴影部分的面积为( ).
A.3 B.4 C.6 D.8

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com