
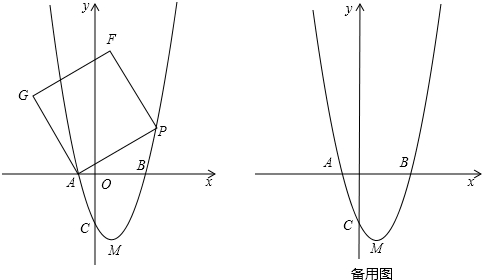
分析 (1)利用抛物线的平移规律即可求得h和k的值;然后令y=0即可求得与x轴的交点坐标;
(2)首先求得点C和点M的坐标,然后求得BC、CM及BM的长,最后利用勾股定理逆定理判定直角三角形即可;
(3)分两AB为边和AB为对角线两种情况讨论计算即可.
(4)分别根据当点G在y轴上时和点F在y轴上时两种情况利用△AOG≌△PHA和△AMP≌△FNP求得点P的坐标即可.
解答 解:(1)∵抛物线y=x2先向右平移1个单位,再向下平移4个单位,得到抛物线y=(x-1)2-4,
∴h=1,k=-4;
令y=0,即(x-1)2-4=0
解得x=-1或x=3,
∴A(-1,0),B (3,0),
(2)∵令x=0,得y=(0-1)2-4=-3,
∴点C的坐标为(0,-3),点M的坐标为(1,-4)
∴BC=3$\sqrt{2}$,MC=$\sqrt{2}$,BM=2$\sqrt{5}$
∴BC2+MC2=BM2
∴△BMC是直角三角形;
∴S=$\frac{1}{2}$BC•CM=$\frac{1}{2}$×3$\sqrt{2}$×$\sqrt{2}$=3;
(3)由(1)知,抛物线y=(x-1)2-4=x2-2x-3,
∵点P是抛物线上一动点,
∴设P(p,p2-2p-3),
∵点Q在y轴上,
∴设Q(0,m),
∵A(-1,0),B(3,0),
∴AB=4,AB的中点M(1,0)
∵点A,B,P,Q组成的四边形是平行四边形,
①当AB为边时,AB∥PQ,AB=PQ,
∴p2-2p-3=m,|p|=4,
Ⅰ、当p=4时,m=5,
∴P(4,5),
Ⅱ、当p=-4时,m=21,
∴P(-4,21)
②当AB为对角线时,点M是PQ的中点,
∴p=2,p2-2p-3+m=0,
∴p=2,m=3,
∴P(2,-3),
∴点P的坐标为(4,5),(-4,21)或(2,-3),
(4)①如图(1),(2)当点G在y轴上时,

由△AOG≌△PHA,
得PH=OA,得yP=xA=-1,
∴x2-2x-3=-1,
得x=1±$\sqrt{2}$,
∴P1(1-$\sqrt{2}$,-1),P2(1+$\sqrt{2}$,-1)
②如图(3),
当点F在y轴上时,由△AMP≌△FNP,
得PM=PN,得yP=xP,
则x2-2x-3=x,
得x=$\frac{3+\sqrt{21}}{2}$,x=$\frac{3-\sqrt{21}}{2}$(舍去),
故P3($\frac{3+\sqrt{21}}{2}$,$\frac{3+\sqrt{21}}{2}$)..
点评 此题是二次函数综合题,主要抛物线的平移的性质,直角三角形的判定,平行四边形的性质,三角形的面积公式,全等三角形的判定和性质,解本题的关键是分类讨论思想,是一道难度比较大的中考常考题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
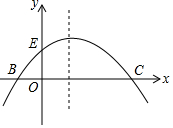 如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(其中m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.
如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(其中m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A,B是数轴上两点(点B在点A右边),O为原点,点A对应着数8,AB=4.解答下列问题:
如图,已知点A,B是数轴上两点(点B在点A右边),O为原点,点A对应着数8,AB=4.解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com