
分析 (1)由方程有两个不相等的实数根结合根的判别式,即可得出△=4-4m>0,解之即可得出m的取值范围;
(2)根据根与系数的关系可得出x1+x2=2、x1x2=m,结合x1+x2-x1x2=6可得出关于m的一元一次方程,解之即可得出结论.
解答 解:(1)∵关于x的方程x2-2x+m=0有两个不相等的实数根x1,x2,
∴△=(-2)2-4m=4-4m>0,
解得:m<1.
(2)∵方程x2-2x+m=0的两根为x1,x2,
∴x1+x2=2,x1x2=m.
∵x1+x2-x1x2=6,
∴2-m=6,
∴m=-4.
点评 本题考查了根的判别式以及根与系数的关系,解题的关键是:(1)牢记“当△>0时,方程有两个不相等的实数根”;(2)根据根与系数的关系结合x1+x2-x1x2=6,找出关于m的一元一次方程.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
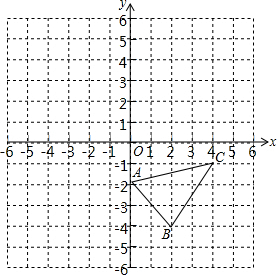 如图,平面直角坐标系中△ABC,分别画出与△ABC关于x轴、y轴对称的△A1B1C1和△A2B2C2,并写出△A1B1C1和△A2B2C2各顶点坐标.
如图,平面直角坐标系中△ABC,分别画出与△ABC关于x轴、y轴对称的△A1B1C1和△A2B2C2,并写出△A1B1C1和△A2B2C2各顶点坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
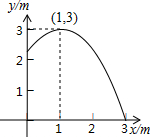 如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )
如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )| A. | 2.1m | B. | 2.2m | C. | 2.3m | D. | 2.25m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com