
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�����A���� ![]() ��0��������ֱ�߷ֱ�y����B��C���㣬��B��C�����������ֱ���һԪ���η���x2��2x��3=0��������
��0��������ֱ�߷ֱ�y����B��C���㣬��B��C�����������ֱ���һԪ���η���x2��2x��3=0��������
��1�����߶�BC�ij��ȣ�
��2�����ʣ�ֱ��AC��ֱ��AB�Ƿ�ֱ����˵�����ɣ�
��3������D��ֱ��AC�ϣ���DB=DC����ֱ��BD�Ľ���ʽ��
��4����x�����Ƿ����P��ʹ��O��B��P����Ϊ��������������ABC���ƣ������ڣ���ֱ��д��P������ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺����x2��2x��3=0�ã�
��x1=3��x2=��1
��B��0��3����C��0����1����
��BC=4��
��2��
�⣺���ۣ�AC��AB���������£�
��A�� ![]() ��0����B��0��3����C��0����1����
��0����B��0��3����C��0����1����
��OA= ![]() ��OB=3��OC=1��
��OB=3��OC=1��
��tan��ABO= ![]() =
= ![]() ��tan��ACO=
��tan��ACO= ![]() =
= ![]() ��
��
���ABO=30�㣬��ACO=60�㣬
���BAC=90�㣬
��AC��AB
��3��
�⣺��ͼ1�У���D��DE��x����E��
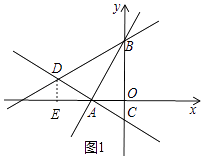
���DEA=��AOC=90�㣬
��tan��ACO= ![]() =
= ![]() ��
��
�ߡ�DCB=60��
��DB=DC��
���DBC�ǵȱ������Σ�
��BA��DC��
��DA=AC��
�ߡ�DAE=��OAC��
���ADE�ա�ACO��
��DE=OC=1��AE=OA= ![]()
�� ![]() ��
��
��D�������� ![]() ��1����
��1����
��ֱ��BD�Ľ���ʽΪy=kx+b������ ![]() ���
��� 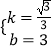 ��
��
��ֱ��BD�Ľ���ʽΪy= ![]() x+3
x+3
��4��
�⣺���ڣ���ͼ2�У��ӳ�BD��x����P1��
�ɣ�3����֪����DBC�ǵȱ������Σ�
���P1BO=60�㣬
���ڡ�ABC�У���ACB=60�㣬��CAB=90�㣬
���P1BC=��ACB=60�㣬�ߡ�P1OB=��CAB=90�㣬
���P1BO�ס�BCA��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��OP1=3 ![]() ��
��
��P1����3 ![]() ��0����
��0����
��P2��A�غ�ʱ����BOP2�ס�BAC����ʱP2���� ![]() ��0����
��0����
�ٸ��ݶԳ��Կɵ�P3�� ![]() ��0����P4��3
��0����P4��3 ![]() ��0��Ҳ����������
��0��Ҳ����������
������������P����������3 ![]() ��0����
��0���� ![]() ��0����
��0���� ![]() ��0����3
��0����3 ![]() ��0��
��0��
����������1���з��̼��������B��C���������⣮��2����tan��ABO= ![]() =
= ![]() ��tan��ACO=
��tan��ACO= ![]() =
= ![]() ���Ƴ���ABO=30�㣬��ACO=60�㣬���ɽ�����⣮��3����ͼ1�У���D��DE��x����E���ɡ�ADE�ա�ACO���Ƴ�DE=OC=1��AE=OA=
���Ƴ���ABO=30�㣬��ACO=60�㣬���ɽ�����⣮��3����ͼ1�У���D��DE��x����E���ɡ�ADE�ա�ACO���Ƴ�DE=OC=1��AE=OA= ![]() �������D���꣬���ô���ϵ�������ɽ�����⣮��4�����ڣ���ͼ2�У��ӳ�BD��x����P1 �� ����֤��P1������������P2��A�غ�ʱҲ�����������ٸ��ݶԳ���д��P3��P4���꼴�ɣ�
�������D���꣬���ô���ϵ�������ɽ�����⣮��4�����ڣ���ͼ2�У��ӳ�BD��x����P1 �� ����֤��P1������������P2��A�غ�ʱҲ�����������ٸ��ݶԳ���д��P3��P4���꼴�ɣ�
�����㾫����������Ĺؼ���������һ�κ��������ʵ����֪ʶ������һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С���Լ���һ�κ�����ͼ������ʵ����⣬�˽�һ�κ�����ֱ�ߣ�ͼ�������ޣ���������������,����ԭ��һֱ�ߣ�����ϵ��k��b,����֮��ĪС����k��б�ʶ��н�,b��Y�������,kΪ��������б,x����y������kΪ��������չ,�仯�������෴��k�ľ���ֵԽ��,��������ԽԶ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MAN=16�㣬A1����AM�ϣ���AN��ȡһ��A2��ʹA2A1=AA1������AM��ȡһ��A3ʹA3A2=A2A1�����һֱ����ȥ������������Ϊֹ����ô���������һ���ǣ�������

A. A5 B. A6 C. A7 D. A8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�½���վվǰ�㳡��Ҫ�̻������Ϊ46000��2 �� ʩ�������̻���22000��2��ÿ��Ĺ���������Ϊԭ����1.5���������ǰ4������˸����̻����̣� 
��1�������̻�����ԭ�ƻ�ÿ����ɶ�����2��
��2�������̻���������һ�鳤Ϊ20�ף���Ϊ8�ľ��οյأ��ƻ���������������ͬ�ľ����̵أ����ǵ����֮��Ϊ56m2 �� �����̵�֮�估�ܱ����п�����ȵ�����ͨ������ͼ��ʾ����������ͨ���Ŀ����Ƕ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ�������У�������ABCD��������BEFG����ԭ��OΪλ�����ĵ�λ��ͼ�Σ������Ʊ�Ϊ ![]() ����A��B��E��x���ϣ���������BEFG�ı߳�Ϊ6����C������Ϊ�� ��
����A��B��E��x���ϣ���������BEFG�ı߳�Ϊ6����C������Ϊ�� �� 
A.��3��2��
B.��3��1��
C.��2��2��
D.��4��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ڡ�ABC�У�AB=AC��DΪBC�ߵ��е㣬����D��DE��AB��DF��AC������ֱ�ΪE��F��

��1����֤��DE=DF��
��2������A=60�㣬BE=1�����ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������OABC������OA��OC�ֱ���x�ᡢy���ϣ���D��5��3���ڱ�AB�ϣ���CΪ���ģ��ѡ�CDB��ת90�㣬����ת���D�Ķ�Ӧ��D��������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
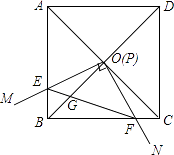
����Ŀ����ͼ���߳�Ϊ1��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����ֱ�ǡ�MPN��ʹֱ�Ƕ���P���O�غϣ�ֱ�DZ�PM��PN�ֱ���OA��OB�غϣ�Ȼ����ʱ����ת��MPN����ת��Ϊ�ȣ�0�㣼�ȣ�90�㣩��PM��PN�ֱ�AB��BC��E��F���㣬����EF��OB�ڵ�G�������н�������ȷ���� ��
��1��EF= ![]() OE����2��S�ı���OEBF��S������ABCD=1��4����3��BE+BF=
OE����2��S�ı���OEBF��S������ABCD=1��4����3��BE+BF= ![]() OA����4������ת�����У�����BEF���COF�����֮�����ʱ��AE=
OA����4������ת�����У�����BEF���COF�����֮�����ʱ��AE= ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����һԲ��ֽƬ���ҡ��������ζ��ۺ�õ���ͼ2��ʾ������AOB����֪OA=6��ȡOA���е�C������C��CD��OA�� ![]() �ڵ�D����F��
�ڵ�D����F�� ![]() ��һ�㣮��������BOD��OD���ۣ���Bǡ�����F�غϣ��ü��������߶�BD��DF��FA���μ��£�����µ�ֽƬ����״ͬ��Ӱͼ�Σ����֮��Ϊ ��
��һ�㣮��������BOD��OD���ۣ���Bǡ�����F�غϣ��ü��������߶�BD��DF��FA���μ��£�����µ�ֽƬ����״ͬ��Ӱͼ�Σ����֮��Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�ֳɱ�Ϊÿ��60Ԫ�ķ�װ���涨�����ڼ����۵��۲����ڳɱ����ۣ��һ������ø���45%�����������֣�������y�����������۵���x��Ԫ������һ�κ���y=kx+b����x=65ʱ��y=55��x=75ʱ��y=45��
��1����һ�κ���y=kx+b�ı���ʽ��
��2�������̳��������ΪWԪ����д������W�����۵���x֮��Ĺ�ϵʽ�����۵��۶�Ϊ����Ԫʱ���̳��ɻ�����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com