
【题目】如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB.已知OA=6,取OA的中点C,过点C作CD⊥OA交 ![]() 于点D,点F是
于点D,点F是 ![]() 上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为 .
上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为 . 
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+x﹣6与x轴两个交点分别是A、B(点A在点B的左侧). 
(1)求A、B的坐标;
(2)利用函数图象,写出y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,过点A(﹣ ![]() ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求直线BD的解析式;
(4)在x轴上是否存在P,使以O、B、P三点为顶点的三角形与△ABC相似?若存在,请直接写出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB是⊙O的直径,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°. 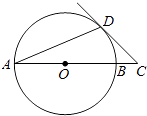
(1)求证:CD是⊙O的切线;
(2)若AB=2 ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)如图1,△ABC为等边三角形,现将三角板中的60°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于30°),旋转后三角板的一直角边与AB交于点D,在三角板斜边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=30°,连接AF,EF.
①求∠EAF的度数;
②DE与EF相等吗?请说明理由;
(2)如图2,△ABC为等腰直角三角形,∠ACB=90°,先将三角板的90°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于45°),旋转后三角板的一直角边与AB交于点D,在三角板另一直角边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=45°,连接AF,EF,请直接写出探究结果:
①求∠EAF的度数;
②线段AE,ED,DB之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义函数f(x),当x≤3时,f(x)=x2﹣2x,当x>3时,f(x)=x2﹣10x+24,若方程f(x)=2x+m有且只有两个实数解,则m的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一牧童在 A 处牧马,牧童的家在 B 处,A,B 处距河岸的距离分别是 AC=500 m,BD=700 m,且 C,D 两地间的距离也为 500 m,天黑前牧童从点 A 将马牵到河边 去饮水,再赶回家,为了使所走的路程最短.
(1)牧童应将马赶到河边的什么地点?请你在图中画出来.
(2)问:他至少要走多少路?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:
港口 | 运费(元/台) | |
甲库 | 乙库 | |
A港 | 14 | 20 |
B港 | 10 | 8 |
(1)设从甲仓库运送到A港口的物资为x吨,求总运费y(元)与x(吨)之间的函数关系式,并写出x的取值范围;
(2)求出最低费用,并说明费用最低时的调配方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com