
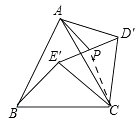
����Ŀ���߳�Ϊ6�ĵȱߡ�ABC�У���D��E�ֱ���AC��BC���ϣ�DE��AB��EC=2 ![]()

��1����ͼ1������DEC�����߷���ƽ�ƣ��õ���D��E��C�䣬��D��E����AC�Ľ���ΪM����C��D�����ACC��Ľ�ƽ���߽��ڵ�N����CC����ʱ���ı���MCND��Ϊ���Σ���˵�����ɣ�
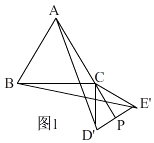
��2����ͼ2������DEC�Ƶ�C��ת�Ϧ���0�㣼����360�㣩���õ���D��E��C������AD�䡢BE�䣮��D��E����е�ΪP��
������ת�����У�AD���BE����������������ϵ����˵�����ɣ�
������AP����AP���ʱ����AD���ֵ��������������ţ�
���𰸡�
��1��
�⣺��CC'= ![]() ʱ���ı���MCND'�����Σ�
ʱ���ı���MCND'�����Σ�
���ɣ���ƽ�Ƶ����ʵã�CD��C'D'��DE��D'E'��
�ߡ�ABC�ǵȱ������Σ�
���B=��ACB=60�㣬
���ACC'=180�㩁��ACB=120�㣬
��CN�ǡ�ACC'�Ľ�ƽ���ߣ�
���D'E'C'= ![]() ��ACC'=60��=��B��
��ACC'=60��=��B��
���D'E'C'=��NCC'��
��D'E'��CN��
���ı���MCND'��ƽ���ı��Σ�
�ߡ�ME'C'=��MCE'=60�㣬��NCC'=��NC'C=60�㣬
���MCE'�͡�NCC'�ǵȱ������Σ�
��MC=CE'��NC=CC'��
��E'C'=2 ![]() ��
��
���ı���MCND'�����Σ�
��CN=CM��
��CC'= ![]() E'C'=
E'C'= ![]()
��2��
�⣺��AD'=BE'��
���ɣ�������180��ʱ������ת�����ʵã���ACD'=��BCE'��
�ɣ�1��֪��AC=BC��CD'=CE'��
���ACD'�ա�BCE'��
��AD'=BE'��
����=180��ʱ��AD'=AC+CD'��BE'=BC+CE'��
����AD'=BE'��
���Ͽ�֪��AD'=BE'��
����ͼ����CP��
�ڡ�ACP�У������������߹�ϵ�ã�AP��AC+CP��
�൱��A��C��P���㹲��ʱ��AP���
��ͼ1���ڡ�D'CE'�У���PΪD'E���е㣬��AP��D'E'��PD'= ![]() ��
��
��CP=3��
��AP=6+3=9��
��Rt��APD'�У��ɹ��ɶ����ã�AD'= ![]() =2
=2 ![]() ��
��
����������1�����жϳ��ı���MCND'Ϊƽ���ı��Σ��������ε����ʵó�CN=CM���������CC'����2���ٷ����������������ת�����ʣ������жϳ���ACD�ա�BCE'���ɵó����ۣ�
�����жϳ���A��C��P���㹲�ߣ������CP��AP������ù��ɶ������ɵó����ۣ�
�����㾫�����������⣬������Ҫ�˽�ȱ������ε�����(�ȱ������ε������Ƕ���Ȳ���ÿ���Ƕ���60��)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�����������ڸ���ϣ�
��1����������ABC����x��ԳƵ�ͼ����A1B1C1��
��2�����A1��B1��C1�������ꣻ
��3������ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=��2����x���һ�������ڣ���3��0���ͣ���4��0��֮�䣬�䲿��ͼ����ͼ��ʾ�������н��ۣ���4a��b=0����c��0���۩�3a+c��0����4a��2b��at2+bt��tΪʵ�������ݵ㣨�� ![]() ��y1��������
��y1�������� ![]() ��y2��������
��y2�������� ![]() ��y3���Ǹ��������ϵĵ㣬��y1��y2��y3 �� ��ȷ�ĸ����У� ��
��y3���Ǹ��������ϵĵ㣬��y1��y2��y3 �� ��ȷ�ĸ����У� �� 
A.4��
B.3��
C.2��
D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��СӨ��С��ʿ���壬СӨִԲ�ӣ�С��ʿִ���ӣ���ͼ���������ķ��ӵ�λ���ã���1��0����ʾ�����½Ƿ��ӵ�λ���ã�0����1����ʾ��СӨ����4öԲ�ӷ������̺��������ӹ���һ����Գ�ͼ�Σ����ŵ�λ���ǣ� ��
A.����2��1��
B.����1��1��
C.��1����2��
D.����1����2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����УΪ�˽���꼶��ͬѧ����������������������ȡ������ͬѧ������1000���ܲ����ԣ����ճɼ���Ϊ���㡢���á��ϸ��벻�ϸ��ĸ��ȼ���ѧУ���������²�������ͳ��ͼ�� 
��1�����ݸ�������Ϣ����ȫ����ͳ��ͼ��
��2����У���꼶��600������������Ƴɼ�δ�ﵽ�����ж�������
��3��ij��ס�����λ�ɼ������ͬѧ��ѡ�вμӼ������е�ѧУ�˶���1000�ױ�����Ԥ���ֱ�ΪA��B��C������У�ѡ���ɳ�ǩȷ�����飮�ס�������ǡ�÷���ͬһ��ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ά��������Ȩ�ͺ���Ȩ�������ಿ�Ŷ��ҹ��캣ʵ���˳�̬��Ѳ����������ͼ������ִ��Ѳ������ĺ��ബ��ÿСʱ50������ٶ������������У���A����õ���P�ڱ�ƫ��60�㷽���ϣ���������1Сʱ����B������ʱ��õ���P�ڱ�ƫ��30�㷽���ϣ�
��1�����APB�Ķ�����
��2����֪�ڵ���P����Χ25�������а������ʺ��ബ�����������������Ƿ�ȫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�E��BC�е㣬AD�ǡ�BAC��ƽ���ߣ�EF//AD��AC��F����AB=11��AC=15����FC�ij�Ϊ�� ��
A.11
B.12
C.13
D.14
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���շ��ź���ѳ�Ϊ������Ⱥ���н�����ϵ����ǿ�����һ���֣����������������˫��̥��������һ��ͯ���ڼ�ĶԻ��� 
���ʣ�
��1��2015�굽2017�����������������һ�յ���������������Ƕ��٣�
��2��2017����һ����������ø��յ��˶���Ǯ���ź����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}��ǰn��n��N*�����ΪSn �� a3=3���Ҧ�Sn=anan+1 �� �ڵȱ�����{bn}�У�b1=2�ˣ�b3=a15+1�� ����������{an}��{bn}��ͨ�ʽ��
����������{cn}��ǰn��n��N*�����ΪTn �� �� ![]() ����Tn ��
����Tn ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com